


Nächste Seite: SUSY-Modelle
Aufwärts: Supersymmetrische Erweiterungen
Vorherige Seite: Supersymmetrische Erweiterungen
Motivation
Das Standardmodell wie unter ![[*]](file:/share/latex2html/devel/icons/crossref.gif) besprochen wirft einige Probleme
auf, die im folgenden kurz angedeutet werden sollen. Ein möglicher
Lösungsansatz für diese Probleme ist die Supersymmetrie (im folgenden kurz:
,,SUSY``genannt), welche eine
Verbindung zwischen Bosonen und Fermionen herstellt. Dieses wurde bereits in
den beiden vorhergehenden Seminarvorträgen besprochen.
besprochen wirft einige Probleme
auf, die im folgenden kurz angedeutet werden sollen. Ein möglicher
Lösungsansatz für diese Probleme ist die Supersymmetrie (im folgenden kurz:
,,SUSY``genannt), welche eine
Verbindung zwischen Bosonen und Fermionen herstellt. Dieses wurde bereits in
den beiden vorhergehenden Seminarvorträgen besprochen.
Ein Problem stellt die Vereinigung der Quantenfeldtheorie mit der
Allgemeinen Relativitätstheorie dar. Daß hier Schwierigkeiten auftreten, kann
man sich zunächst anschaulich dadurch erklären, daß in der
Relativitätstheorie die Energie (oder äquivalent die Masse) die Quelle eines
Gravitationsfeldes ist, in der Quantenmechanik jedoch aufgrund der
Heisenbergschen Unschärferelation die Energie unbestimmt ist. Es können für
infinitesimal kleine Zeiten unendliche Werte für die Energie angenommen
werden. Somit entsteht auch eine unendliche Quelle für das
Gravitationsfeld.
Genauer ist der Zusammenhang zwischen der Allgemeinen
Relativitätstheorie, deren Symmetriegruppe die Poincaré Gruppe ist, und dem
Standardmodell, welches von Inneren Symmetrien ausgeht, gerade im Zusammenhang
mit der Vereinheitlichung dieser Symmetrien untersucht worden. Dabei stellte
sich heraus, daß eine Vereinheitlichung nur möglich ist, wenn man auch
Symmetriegruppen zuläßt, deren Algebra auf Antikommutatoren beruht. Dies
wird gerade durch die Supersymmetrie ermöglicht. Dies soll nun vereinfacht
dargestellt werden: Ähnlich wie in der Isospin-Symmetrie sind in der SUSY die
Boson- und Fermionfelder miteinander verbunden. Beschreibe 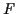 das
Fermionenfeld und
das
Fermionenfeld und 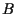 das Bosonenfeld. Eine SUSY-Transformation
das Bosonenfeld. Eine SUSY-Transformation 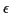 bewirkt nun folgendes:
bewirkt nun folgendes:
Die Aufenthaltswahrscheinlichkeit eines Teilchen wird nun gerade durch den
Wert des Feldes beschrieben. Daraus ergibt sich sofort
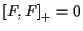 (da
(da
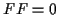 gelten muß: die Aufenthaltswahrscheinlichkeit zweier Fermionen am
selben Ort ist null.) Für das Bosonenfeld muß dies nicht notwendig gelten,
gelten muß: die Aufenthaltswahrscheinlichkeit zweier Fermionen am
selben Ort ist null.) Für das Bosonenfeld muß dies nicht notwendig gelten,
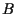 darf kommutieren. Allerdings muß gefordert werden:
darf kommutieren. Allerdings muß gefordert werden:
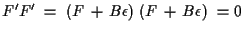
Dies wird durch
gewährleistet.
Somit ist die geforderte Formulierung durch Antikommutatoren
gewährleistet. Um dies noch etwas genauer zu betrachten, führen wir zunächst den
Begriff der Graduierten Algebra ein (vgl. hierzu und dem folgenden
[Kal97], Kap. 9). Eine  Graduierte Algebra besteht aus einem
Vektorraum
Graduierte Algebra besteht aus einem
Vektorraum
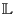 , der als direkte Summe aus
, der als direkte Summe aus 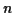 Unterräumen
Unterräumen
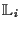 gechrieben werden kann:
gechrieben werden kann:
und einem Produkt 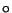 mit den Eigenschaften:
mit den Eigenschaften:
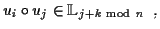
mit:
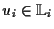
Für unsere Betrachtungen erweisen sich gerade 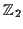 graduierte Algebren als
nützlich. Deshalb wird noch speziell die
graduierte Algebren als
nützlich. Deshalb wird noch speziell die 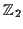 graduierte Liealgebra
definiert. Hierbei gelten für das Produkt
graduierte Liealgebra
definiert. Hierbei gelten für das Produkt 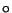 die folgenden
Eigenschaften:
die folgenden
Eigenschaften:
| Graduierung: |
|
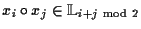 |
|
| Supersymmetrie: |
|
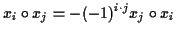 |
|
| |
|
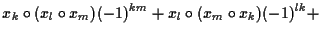 |
|
| |
|
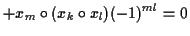 |
|
wobei
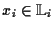 und
und
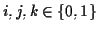 . Das besondere hierbei
ist, daß das Produkt wegen der Forderung der sogenannten Supersymmetrie
sowohl symmetrisch als auch antisymmetrisch sein kann. Die Elemente aus
. Das besondere hierbei
ist, daß das Produkt wegen der Forderung der sogenannten Supersymmetrie
sowohl symmetrisch als auch antisymmetrisch sein kann. Die Elemente aus
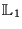 werden als SUSY-Generatoren bezeichnet. Deren Anzahl
werden als SUSY-Generatoren bezeichnet. Deren Anzahl 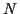 ist
definiert als
ist
definiert als
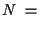
dim
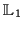
Nun wollen wir uns die Superalgebra, d.h. die 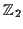 -Graduierung, der
Poincaré-Gruppe (diese Gruppe wird noch in einem späteren Vortrag des
Seminars behandelt) ansehen. Die Poincaré-Gruppe spanne mit ihren 10
Generatoren
-Graduierung, der
Poincaré-Gruppe (diese Gruppe wird noch in einem späteren Vortrag des
Seminars behandelt) ansehen. Die Poincaré-Gruppe spanne mit ihren 10
Generatoren 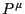 (Translationen) und
(Translationen) und
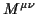 (Lorentzgruppe) den
Unterraum
(Lorentzgruppe) den
Unterraum
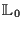 auf, dieser werde durch
auf, dieser werde durch 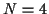 SUSY-Generatoren
SUSY-Generatoren 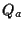 erweitert. Diese Generatoren sollen nun die Eigenschaften einer graduierten
Liealgebra erfüllen. Dazu müssen die Verknüpfungen
erweitert. Diese Generatoren sollen nun die Eigenschaften einer graduierten
Liealgebra erfüllen. Dazu müssen die Verknüpfungen
entsprechend definiert werden. Eine mögliche Wahl liefert dann die
Poincaré-Algebra:
(die Definitionen sind im einzelnen in [Kal97] nachzulesen um den
Rahmen dieses Überblickes nicht zu sprengen.)
Das überraschendste Ergebnis hierbei ist wohl die letzte der obigen
Relationen. Danach führen nämlich zwei SUSY-Transformationen nacheinander
durchgeführt zu einer Translation in der Raum-Zeit! Somit ist also ein
Zusammenhang zwischen der Supersymmetrie und der Allgemeinen
Relativitätstheorie zu erwarten, da diese gerade die Poincaré-Invarianz als
Eichsymmetrie enthält.
Nun soll, bevor einige Ansätze zur Erweiterung des Standardmodells
vorgestellt werden, noch kurz angemerkt werden, wie Lagrange-Dichten
supersymmetrisch formuliert werden können. Dies ist sicherlich in einem
SUSY-Modell erforderlich, will man den beim Standardmodell bisher so
erfolgreichen Formalismus auch hier anwenden. Zunächst ist die Einführung
sogenannter Superzahlen erforderlich (dies ist noch als Vortragsthema für
einen späteren Vortrag vorgesehen, deshalb wird hier nur kurz über den
Ansatz referiert, nachzulesen in [Kal97], Kap. 4):
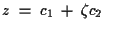
mit:
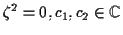
Hierbei wird 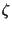 als Generator bezeichnet (i.a. existieren mehrere
Generatoren, die dann einer sogenannten Grassmann-Algebra genügen). Im
Superraum-Konzept werden nun den normalen Dimensionen Superraumdimensionen
hinzugefügt, ein Feld besteht dann aus normalen Feldern und Superfeldern:
(Anm.: das erste Beispiel kann als Taylor-Entwicklung des Superfeldes nach
als Generator bezeichnet (i.a. existieren mehrere
Generatoren, die dann einer sogenannten Grassmann-Algebra genügen). Im
Superraum-Konzept werden nun den normalen Dimensionen Superraumdimensionen
hinzugefügt, ein Feld besteht dann aus normalen Feldern und Superfeldern:
(Anm.: das erste Beispiel kann als Taylor-Entwicklung des Superfeldes nach
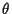 angesehen werden, die exakt nach dem 2. Term abbricht.)
Mit diesen Superfeldern wird dann die Lagrangedichte zu formulieren sein.
angesehen werden, die exakt nach dem 2. Term abbricht.)
Mit diesen Superfeldern wird dann die Lagrangedichte zu formulieren sein.



Nächste Seite: SUSY-Modelle
Aufwärts: Supersymmetrische Erweiterungen
Vorherige Seite: Supersymmetrische Erweiterungen
root
1999-12-14
![]() das
Fermionenfeld und
das
Fermionenfeld und ![]() das Bosonenfeld. Eine SUSY-Transformation
das Bosonenfeld. Eine SUSY-Transformation ![]() bewirkt nun folgendes:
bewirkt nun folgendes:
![]() Graduierte Algebra besteht aus einem
Vektorraum
Graduierte Algebra besteht aus einem
Vektorraum
![]() , der als direkte Summe aus
, der als direkte Summe aus ![]() Unterräumen
Unterräumen
![]() gechrieben werden kann:
gechrieben werden kann: