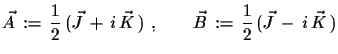 |
(3.1) |
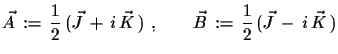 |
(3.1) |
| (3.2) |
![$\displaystyle \shadowbox{
$[A^{k},\,B^{l}]\,=\,0$}\,\,.$](img223.gif) |
(3.3) |
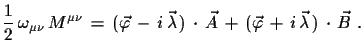 |
(3.4) |
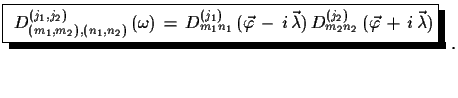 |
(3.5) |
| (3.6) |
| (3.7) | ||
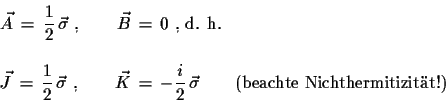 |
(3.8) |
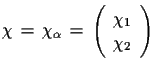 |
(3.9) |
| (3.10) |
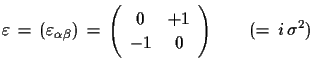 |
(3.11) |
| (3.12) |
| (3.13) |
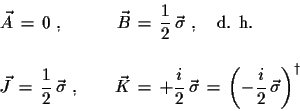 |
(3.14) |
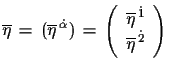 (,,gepunktete`` Indizes bzw. Spinoren) (,,gepunktete`` Indizes bzw. Spinoren) |
(3.15) |
| (3.16) |
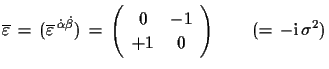 |
(3.17) |
| (3.18) |
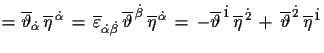 |
||
| (3.19) |
| (3.20) |
| (3.21) |
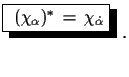 |
(3.22) |
| (3.23) |
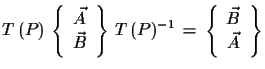 |
(3.24) |
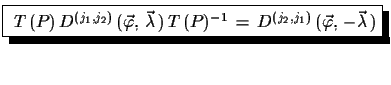 |
(3.25) |
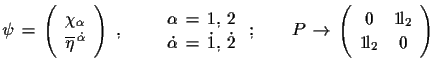 |
(3.27) |
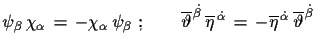 |
(3.28) |
| (3.29) |
| (3.30) |