



Nächste Seite: Literatur
Aufwärts: Optionspreise nach Black-Scholes
Vorherige Seite: Die Black-Scholes -Differentialgleichung
Inhalt
Zur Berechnung des Preises einer
(europäischen) Call-Option
müssen daher als erstes die entsprechenden Randbedingungen
festgelegt werden.
Zum Fälligkeitstermin gilt
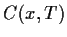 = max
= max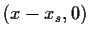 .
Bei einem Underlyingkurs von 0
ist es nie lohnend das Optionsrecht wahrzunehmen.
Da weiterhin ein Kurs von 0
unter einem log-normalem Model sich nicht mehr verändert
gilt also für alle Zeiten
.
Bei einem Underlyingkurs von 0
ist es nie lohnend das Optionsrecht wahrzunehmen.
Da weiterhin ein Kurs von 0
unter einem log-normalem Model sich nicht mehr verändert
gilt also für alle Zeiten
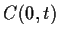 = 0.
Im Limes
= 0.
Im Limes
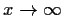 lohnt es sich die Option einzulösen.
Bei europäischen Optionen ist dies
jedoch nur zum Fälligkeitstermin möglich.
Berücksichtigung des Zinsfaktors liefert
lohnt es sich die Option einzulösen.
Bei europäischen Optionen ist dies
jedoch nur zum Fälligkeitstermin möglich.
Berücksichtigung des Zinsfaktors liefert
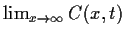 =
=
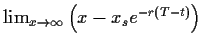 =
= 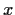 .
.
Um die Black-Scholes-Differentialgleichung (72)
zu vereinfachen, substituieren wir nun
- 1.
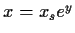 ,
um von log-normal zu normalverteilten Größen
überzugehen, d.h um die Potenzen von
,
um von log-normal zu normalverteilten Größen
überzugehen, d.h um die Potenzen von 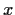 vor den Ableitungstermen
zum Verschwinden zu bringen,
vor den Ableitungstermen
zum Verschwinden zu bringen,
- 2.
-
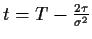 ,
um eine dimensionslose Variable
,
um eine dimensionslose Variable 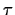 zu bekommen und
um das Endwertproblem bzgl.
zu bekommen und
um das Endwertproblem bzgl. 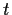 in ein Anfangswertproblem
bzgl.
in ein Anfangswertproblem
bzgl. 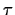 zu überführen,
zu überführen,
- 3.
- sowie
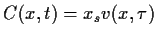 um eine dimensionslose Preisvariable zu erhalten.
um eine dimensionslose Preisvariable zu erhalten.
Gl. (72) wird nun
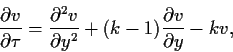 |
(73) |
mit nur einem dimensionslosen Parameter
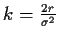 ,
und der Randbedingung
,
und der Randbedingung
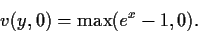 |
(74) |
Um neben der Zeitableitung
nur einen Term mit zweiter Ableitung überzubehalten
verwenden wir den Ansatz,
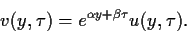 |
(75) |
Eingesetzt in Gl.(74) entsteht,
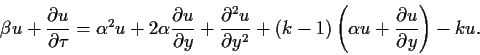 |
(76) |
Die niedrigeren Ableitungsterme verschwinden, wenn
Dies läßt sich auflösen nach 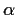 ,
, 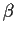
so daß also bei der Wahl von 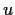 mit
mit
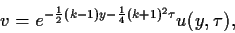 |
(81) |
aus (72) die
Diffusionsgleichung wird
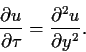 |
(82) |
Hierbei ist
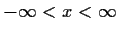 ,
,
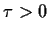 ,
und es gilt die Randbedingung
,
und es gilt die Randbedingung
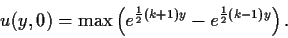 |
(83) |
Die Lösung der Diffusionsgleichung ist wohlbekannt
(Nachprüfen durch Einsetzen, oder alternativ,
durch Lösen durch Fouriertransformation).
Für ein Anfangswertproblem
lautet die Lösung der Diffusionsgleichung
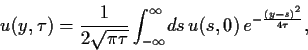 |
(84) |
wobei 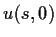 die Anfangswertverteilung aus Gl. (84)
bezeichnet.
Die max--Funktion kappt die untere Integrationsgrenze,
und das resultierende
Integral ist uns bei der Behandlung des Zuganges von
Bouchaud-Sornette-Potters schon begegnet.
Rückführung auf das Integral
die Anfangswertverteilung aus Gl. (84)
bezeichnet.
Die max--Funktion kappt die untere Integrationsgrenze,
und das resultierende
Integral ist uns bei der Behandlung des Zuganges von
Bouchaud-Sornette-Potters schon begegnet.
Rückführung auf das Integral 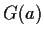 in (87)
und
Rücksubstitution der Orginalvariablen
liefert genau wie dort
die Black-Scholes-Formel für eine europäische Call-Option,
in (87)
und
Rücksubstitution der Orginalvariablen
liefert genau wie dort
die Black-Scholes-Formel für eine europäische Call-Option,
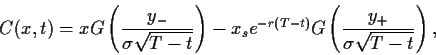 |
(85) |
mit
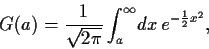 |
(86) |
und
Die Abhängigkeiten des resultierenden Preises
von den verschiedenen Parametern haben wir bereits ausführlich
in der letzten Vorlesung diskutiert.
Wir fassen abschließend nocheinmal die Voraussetzungen, die dem
Ansatz von Black-Scholes zugrunde liegen, zusammen:
- 1.
- Keine Arbitragemöglichkeit
- 2.
- Log-normal verteilte Aktienkurse
- 3.
- Zinsrate
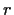 ist bekannt
ist bekannt
- 4.
- Volatilität
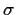 ist bekannt
ist bekannt
- 5.
- Keine Transaktionskosten
- 6.
- Kontinuierliches Handeln möglich
- 7.
- Shortselling ist erlaubt
- 8.
- Aktien sind beliebig teilbar
- 9.
- Keine Dividenden
Mehr pragmatisch orientierte Informationen zum Handel mit Derivaten
findet man in
[14,3,4].
Eine Sammlung von Optionspreisformeln (ohne Herleitungen)
für verschiedenartigste Optionen ist
[10].
Abschließend bemerken wir noch, daß die Black-Scholes-Formel
von einer Kenntnis der Volatilität 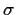 ausgeht.
Empirisch zugänglich sind jedoch nur die historischen Volatilitäten,
wie sie den Kursentwicklungen der Vergangenheit entnommen werden können.
Die von den Marktteilnehmern für die Zukunft erwarteten Volatilitäten
können davon jedoch wesentlich verschieden sein.
In der Tat, unterscheiden sich die historischen Volatilitäten
deutlich von den ``impliziten'' Volatilitäten,
d.h. denjenigen die sich aus den tatsächlichen Optionspreisen unter Annahme
der Black-Scholes-Formel ergeben
[6,5].
Diese Abweichungen zwischen historischen und impliziten Volatilitäten
können teilweise auch als Korrekturen des Marktes
aufgefaßt werden,
die beispielsweise
der Abweichung der tatsächlichen Verteilung der Aktienkurse
(z.B. lange Schwänze) von der der Black-Scholes-Formel zugrunde liegenden
Log-Normal-Verteilung
Rechnung tragen.
ausgeht.
Empirisch zugänglich sind jedoch nur die historischen Volatilitäten,
wie sie den Kursentwicklungen der Vergangenheit entnommen werden können.
Die von den Marktteilnehmern für die Zukunft erwarteten Volatilitäten
können davon jedoch wesentlich verschieden sein.
In der Tat, unterscheiden sich die historischen Volatilitäten
deutlich von den ``impliziten'' Volatilitäten,
d.h. denjenigen die sich aus den tatsächlichen Optionspreisen unter Annahme
der Black-Scholes-Formel ergeben
[6,5].
Diese Abweichungen zwischen historischen und impliziten Volatilitäten
können teilweise auch als Korrekturen des Marktes
aufgefaßt werden,
die beispielsweise
der Abweichung der tatsächlichen Verteilung der Aktienkurse
(z.B. lange Schwänze) von der der Black-Scholes-Formel zugrunde liegenden
Log-Normal-Verteilung
Rechnung tragen.




Nächste Seite: Literatur
Aufwärts: Optionspreise nach Black-Scholes
Vorherige Seite: Die Black-Scholes -Differentialgleichung
Inhalt
Joerg_Lemm
2000-02-25
![]() = max
= max![]() .
Bei einem Underlyingkurs von 0
ist es nie lohnend das Optionsrecht wahrzunehmen.
Da weiterhin ein Kurs von 0
unter einem log-normalem Model sich nicht mehr verändert
gilt also für alle Zeiten
.
Bei einem Underlyingkurs von 0
ist es nie lohnend das Optionsrecht wahrzunehmen.
Da weiterhin ein Kurs von 0
unter einem log-normalem Model sich nicht mehr verändert
gilt also für alle Zeiten
![]() = 0.
Im Limes
= 0.
Im Limes
![]() lohnt es sich die Option einzulösen.
Bei europäischen Optionen ist dies
jedoch nur zum Fälligkeitstermin möglich.
Berücksichtigung des Zinsfaktors liefert
lohnt es sich die Option einzulösen.
Bei europäischen Optionen ist dies
jedoch nur zum Fälligkeitstermin möglich.
Berücksichtigung des Zinsfaktors liefert
![]() =
=
![]() =
= ![]() .
.
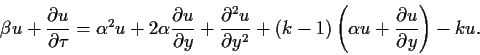
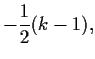
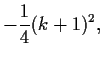
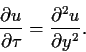
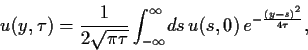
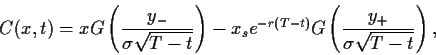
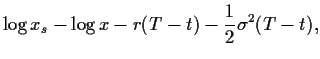
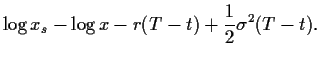
![]() ausgeht.
Empirisch zugänglich sind jedoch nur die historischen Volatilitäten,
wie sie den Kursentwicklungen der Vergangenheit entnommen werden können.
Die von den Marktteilnehmern für die Zukunft erwarteten Volatilitäten
können davon jedoch wesentlich verschieden sein.
In der Tat, unterscheiden sich die historischen Volatilitäten
deutlich von den ``impliziten'' Volatilitäten,
d.h. denjenigen die sich aus den tatsächlichen Optionspreisen unter Annahme
der Black-Scholes-Formel ergeben
[6,5].
Diese Abweichungen zwischen historischen und impliziten Volatilitäten
können teilweise auch als Korrekturen des Marktes
aufgefaßt werden,
die beispielsweise
der Abweichung der tatsächlichen Verteilung der Aktienkurse
(z.B. lange Schwänze) von der der Black-Scholes-Formel zugrunde liegenden
Log-Normal-Verteilung
Rechnung tragen.
ausgeht.
Empirisch zugänglich sind jedoch nur die historischen Volatilitäten,
wie sie den Kursentwicklungen der Vergangenheit entnommen werden können.
Die von den Marktteilnehmern für die Zukunft erwarteten Volatilitäten
können davon jedoch wesentlich verschieden sein.
In der Tat, unterscheiden sich die historischen Volatilitäten
deutlich von den ``impliziten'' Volatilitäten,
d.h. denjenigen die sich aus den tatsächlichen Optionspreisen unter Annahme
der Black-Scholes-Formel ergeben
[6,5].
Diese Abweichungen zwischen historischen und impliziten Volatilitäten
können teilweise auch als Korrekturen des Marktes
aufgefaßt werden,
die beispielsweise
der Abweichung der tatsächlichen Verteilung der Aktienkurse
(z.B. lange Schwänze) von der der Black-Scholes-Formel zugrunde liegenden
Log-Normal-Verteilung
Rechnung tragen.