



Next: Exact predictive density
Up: Regression
Previous: Regression
Contents
An important special case of density estimation
leading to quadratic data terms
is regression for independent training data
with Gaussian likelihoods
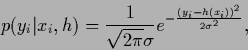 |
(245) |
with fixed, but possibly 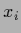 -dependent, variance
-dependent, variance 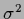 .
In that case
.
In that case  =
=
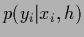 is specified by
is specified by 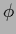 =
= 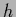 and
the logarithmic term
and
the logarithmic term
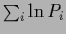 becomes quadratic in the regression function
becomes quadratic in the regression function 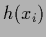 ,
i.e., of the form (225).
In an interpretation as empirical risk minimization
quadratic error terms corresponds to the choice of
a squared error loss function
,
i.e., of the form (225).
In an interpretation as empirical risk minimization
quadratic error terms corresponds to the choice of
a squared error loss function 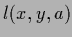 =
= 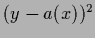 for action
for action
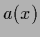 .
Similarly, the
technical analogon of Bayesian priors
are additional (regularizing) cost terms.
.
Similarly, the
technical analogon of Bayesian priors
are additional (regularizing) cost terms.
We have remarked in Section 2.3
that for continuous 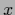 measurement
of
measurement
of 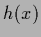 has to be understood as
measurement of a
has to be understood as
measurement of a
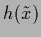 =
=
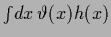 for sharply peaked
for sharply peaked 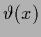 .
We assume here that the discretization
of
.
We assume here that the discretization
of 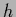 used in numerical calculations takes care of that averaging.
Divergent quantities like
used in numerical calculations takes care of that averaging.
Divergent quantities like 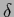 -functionals,
used here for convenience, will then not be present.
-functionals,
used here for convenience, will then not be present.
We now combine Gaussian data terms and a Gaussian (specific) prior
with prior operator
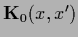 and define for training data
and define for training data 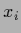 ,
, 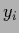 the operator
the operator
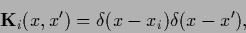 |
(246) |
and training data templates 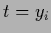 .
We also allow a general prior template
.
We also allow a general prior template 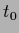 but remark that it is often chosen identically zero.
According to (230) the resulting functional can be written
in the following forms, useful for different purposes,
but remark that it is often chosen identically zero.
According to (230) the resulting functional can be written
in the following forms, useful for different purposes,
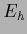 |
 |
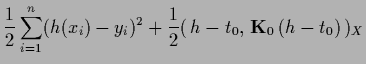 |
(247) |
| |
 |
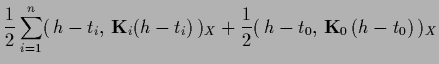 |
(248) |
| |
 |
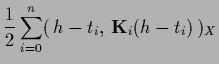 |
(249) |
| |
 |
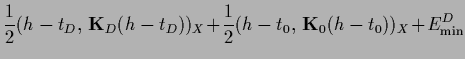 |
(250) |
| |
 |
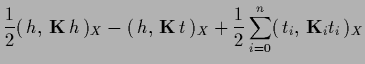 |
(251) |
| |
 |
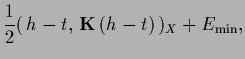 |
(252) |
with
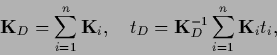 |
(253) |
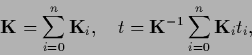 |
(254) |
and
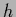 -independent minimal errors,
-independent minimal errors,
being proportional to the ``generalized variances''
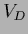 =
=
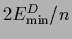 and
and
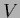 =
=
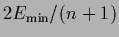 .
The scalar product
.
The scalar product
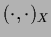 stands for
stands for 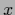 -integration only,
for the sake of simplicity however, we will skip the subscript
-integration only,
for the sake of simplicity however, we will skip the subscript 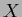 in the following.
The data operator
in the following.
The data operator 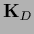
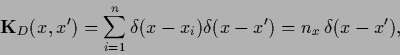 |
(257) |
contains for discrete 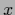 on its diagonal
the number of measurements at
on its diagonal
the number of measurements at 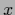 ,
,
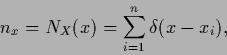 |
(258) |
which is zero for 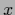 not in the training data.
As already mentioned for continuous
not in the training data.
As already mentioned for continuous 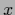 a integration
around a neighborhood of
a integration
around a neighborhood of 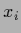 is required.
is required.
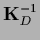 is a short hand notation for
the inverse within the space of training data
is a short hand notation for
the inverse within the space of training data
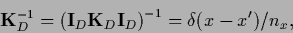 |
(259) |
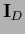 denoting
the projector into the space of training data
denoting
the projector into the space of training data
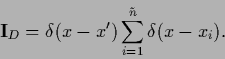 |
(260) |
Notice that the sum is not over all  training points
training points  but only over the
but only over the 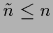 different
different 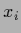 .
(Again for continuous
.
(Again for continuous 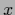 an integration around
an integration around 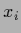 is required
to ensure
is required
to ensure 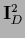 =
= 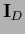 ).
Hence, the data template
).
Hence, the data template
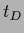 becomes the mean of
becomes the mean of 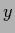 -values measured at
-values measured at 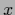
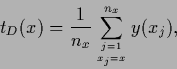 |
(261) |
and 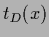 =
=  for
for 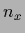 =
= 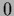 .
Normalization of
.
Normalization of 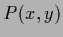 is not influenced by a change in
is not influenced by a change in 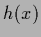 so the Lagrange multiplier terms have been skipped.
so the Lagrange multiplier terms have been skipped.
The stationarity equation is most easily obtained from (252),
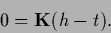 |
(262) |
It is linear and has on a space where
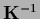 exists
the unique solution
exists
the unique solution
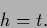 |
(263) |
We remark that 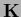 can be invertible
(and usually is so the learning problem is well defined)
even if
can be invertible
(and usually is so the learning problem is well defined)
even if 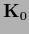 is not invertible.
The inverse
is not invertible.
The inverse
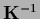 , necessary to calculate
, necessary to calculate 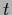 ,
is training data dependent
and represents the covariance operator/matrix
of a Gaussian posterior process.
In many practical cases, however, the prior covariance
,
is training data dependent
and represents the covariance operator/matrix
of a Gaussian posterior process.
In many practical cases, however, the prior covariance
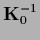 (or in case of a null space a pseudo inverse of
(or in case of a null space a pseudo inverse of 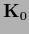 )
is directly given or can be calculated.
Then an inversion of a finite dimensional matrix
in data space is sufficient to find the minimum of the energy
)
is directly given or can be calculated.
Then an inversion of a finite dimensional matrix
in data space is sufficient to find the minimum of the energy 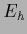 [228,76].
[228,76].
Invertible 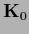 :
Let us first study the case of an invertible
:
Let us first study the case of an invertible 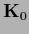 and consider the stationarity equation
as obtained from (248) or (250)
and consider the stationarity equation
as obtained from (248) or (250)
For existing
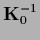
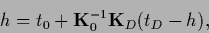 |
(266) |
one can introduce
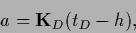 |
(267) |
to obtain
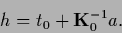 |
(268) |
Inserting Eq. (268) into Eq. (267) one finds
an equation for 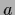
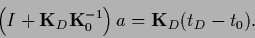 |
(269) |
Multiplying Eq. (269)
from the left by the projector 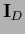 defined in (260)
and using
defined in (260)
and using
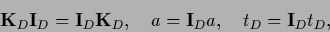 |
(270) |
one obtains an equation in data space
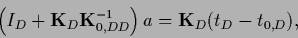 |
(271) |
where
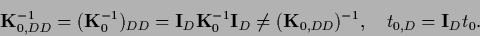 |
(272) |
Thus,
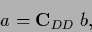 |
(273) |
where
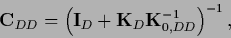 |
(274) |
and
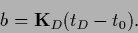 |
(275) |
In components Eq. (273) reads,
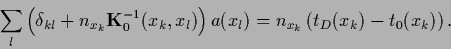 |
(276) |
Having calculated 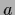 the solution
the solution 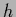 is given by Eq. (268)
is given by Eq. (268)
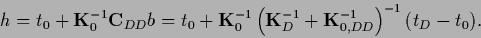 |
(277) |
Eq. (277)
can also be obtained directly from
Eq. (263) and the definitions (254),
without introducing the auxiliary variable 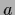 ,
using the decomposition
,
using the decomposition
 =
=
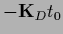 +
+
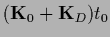 and
and
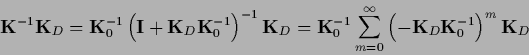 |
(278) |
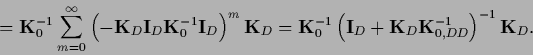 |
(279) |
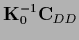 is also known as equivalent kernel
due to its relation to kernel smoothing techniques
[210,94,90,76].
is also known as equivalent kernel
due to its relation to kernel smoothing techniques
[210,94,90,76].
Interestingly,
Eq. (268) still holds
for non-quadratic data terms
of the form 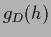 with any differentiable function
fulfilling
with any differentiable function
fulfilling
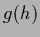 =
= 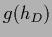 ,
where
,
where 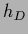 =
= 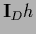 is the restriction of
is the restriction of 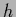 to data space.
Hence, also
the function of functional derivatives
with respect to
to data space.
Hence, also
the function of functional derivatives
with respect to 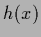 is restricted to data space, i.e.,
is restricted to data space, i.e.,
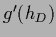 =
=
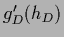 with
with 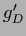 =
=
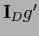 and
and
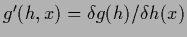 .
For example,
.
For example,
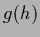 =
=
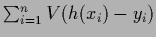 with
with 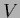 a differentiable function.
The finite dimensional vector
a differentiable function.
The finite dimensional vector 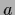 is then found by solving a nonlinear equation instead of a linear one
[73,75].
is then found by solving a nonlinear equation instead of a linear one
[73,75].
Furthermore, one can study vector fields, i.e., the case where,
besides possibly 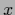 ,
also
,
also 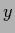 , and thus
, and thus 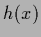 , is a vector for given
, is a vector for given 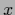 .
(Considering the variable indicating the vector components of
.
(Considering the variable indicating the vector components of 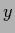 as part of the
as part of the 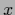 -variable,
this is a situation where a fixed number of one-dimensional
-variable,
this is a situation where a fixed number of one-dimensional 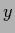 ,
corresponding to a subspace of
,
corresponding to a subspace of 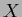 with fixed dimension,
is always measured simultaneously.)
In that case the diagonal
with fixed dimension,
is always measured simultaneously.)
In that case the diagonal 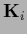 of Eq. (246)
can be replaced by a version with non-zero off-diagonal elements
of Eq. (246)
can be replaced by a version with non-zero off-diagonal elements
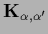 between the vector components
between the vector components  of
of 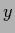 .
This corresponds
to a multi-dimensional Gaussian data generating probability
.
This corresponds
to a multi-dimensional Gaussian data generating probability
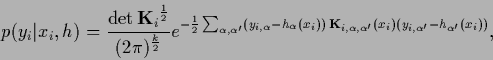 |
(280) |
for 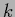 -dimensional vector
-dimensional vector 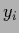 with components
with components 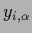 .
.
Non-invertible 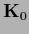 :
For non-invertible
:
For non-invertible 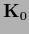 one can solve for
one can solve for 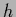 using the Moore-Penrose inverse
using the Moore-Penrose inverse
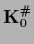 .
Let us first recall some basic facts
[58,164,186,187,126,15,120].
A pseudo inverse
.
Let us first recall some basic facts
[58,164,186,187,126,15,120].
A pseudo inverse 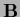 of (a possibly non-square)
of (a possibly non-square) 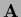 is defined by the conditions
is defined by the conditions
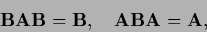 |
(281) |
and becomes for real 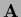 the unique Moore-Penrose inverse
the unique Moore-Penrose inverse 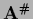 if
if
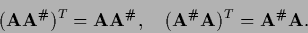 |
(282) |
A linear equation
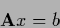 |
(283) |
is solvable if
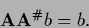 |
(284) |
In that case the solution is
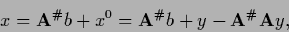 |
(285) |
where
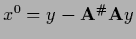 is solution of the homogeneous equation
is solution of the homogeneous equation
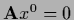 and vector
and vector 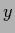 is arbitrary.
Hence,
is arbitrary.
Hence, 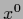 can be expanded in an orthonormalized basis
can be expanded in an orthonormalized basis 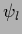 of the null space of
of the null space of 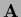
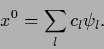 |
(286) |
For a diagonal
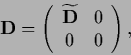 |
(287) |
where
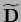 is invertible,
the Moore-Penrose inverse is
is invertible,
the Moore-Penrose inverse is
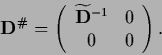 |
(288) |
For a square matrix 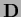 the product
the product
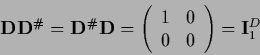 |
(289) |
becomes the projector on the space where
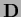 is invertible.
Similarly,
is invertible.
Similarly,
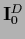 =
=
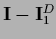 is the projector on the null space of
is the projector on the null space of 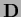 .
.
For a general (possible non-square) 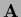 there always exist orthogonal
there always exist orthogonal 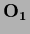 and
and 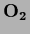 so it can be written in orthogonal normal form
so it can be written in orthogonal normal form
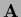 =
=
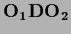 ,
where
,
where 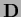 is of the form of Eq. (287)
[120].
The corresponding Moore-Penrose inverse is
is of the form of Eq. (287)
[120].
The corresponding Moore-Penrose inverse is
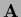 =
=
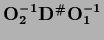 .
.
Similarly, for an 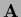 which can be diagonalized, i.e.,
for a square matrix
which can be diagonalized, i.e.,
for a square matrix 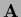 =
=
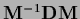 with diagonal
with diagonal 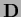 ,
the Moore-Penrose inverse is
,
the Moore-Penrose inverse is
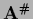 =
=
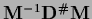 .
From Eq. (289) it follows then that
.
From Eq. (289) it follows then that
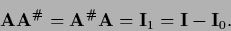 |
(290) |
where
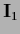 =
=
 =
=
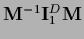 projects on the space where
projects on the space where 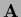 is invertible
and
is invertible
and
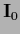 =
=
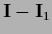 =
=
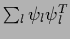 is the projector into the null space of
is the projector into the null space of 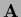 .
Then from the definition (281)
it follows
.
Then from the definition (281)
it follows
 |
(291) |
Sometimes it is convenient to write
in that case
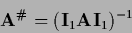 |
(292) |
where the inversion is understood to be performed in the subspace
where 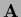 is invertible.
Expressed by projectors the solvability condition Eq. (284)
becomes
is invertible.
Expressed by projectors the solvability condition Eq. (284)
becomes
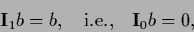 |
(293) |
or in terms of a basis 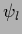 of the null space
of the null space
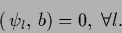 |
(294) |
This means that the inhomogeneity 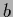 must have no components
within the null space of
must have no components
within the null space of 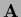 .
Furthermore we can then write
.
Furthermore we can then write
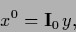 |
(295) |
showing that an 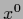 can be obtained by projecting an arbitrary
can be obtained by projecting an arbitrary 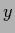 on the null space of
on the null space of 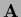 .
Collecting the results for an
.
Collecting the results for an
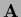 which can be diagonalized,
Eq. (285)
can be expressed in terms of projection operators as follows:
which can be diagonalized,
Eq. (285)
can be expressed in terms of projection operators as follows:
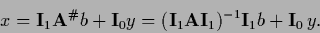 |
(296) |
Thus a solution 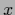 is obtained by inverting
is obtained by inverting 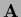 in the subspace where it is invertible
and adding an arbitrary component of the null space.
in the subspace where it is invertible
and adding an arbitrary component of the null space.
Now we apply this to Eq. (265)
where 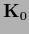 is
diagonalizable because being positive semi-definite.
(In this case
is
diagonalizable because being positive semi-definite.
(In this case 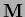 is an orthogonal matrix
and the entries of
is an orthogonal matrix
and the entries of 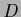 are real and larger or equal to zero.)
Hence, one obtains under the condition
are real and larger or equal to zero.)
Hence, one obtains under the condition
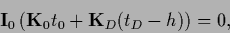 |
(297) |
for Eq. (285)
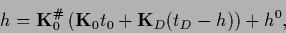 |
(298) |
where
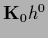 =
= 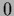 so that
so that
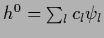 can be expanded in an orthonormalized basis
can be expanded in an orthonormalized basis 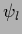 of the null space of
of the null space of 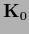 , assumed here
to be of finite dimension.
To find an equation in data space
define the vector
, assumed here
to be of finite dimension.
To find an equation in data space
define the vector
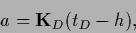 |
(299) |
to get from Eqs.(297) and (298)
These equations have to be solved for 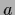 and the coefficients
and the coefficients 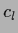 .
Inserting Eq. (301) into the
definition (299) gives
.
Inserting Eq. (301) into the
definition (299) gives
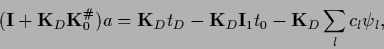 |
(302) |
using
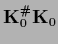 =
= 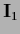 according to Eq. (290).
Using
according to Eq. (290).
Using 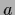 =
=  [where
[where 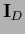 ,
the projector on the space of training data,
is defined in (260)]
the solvability condition (297) becomes
,
the projector on the space of training data,
is defined in (260)]
the solvability condition (297) becomes
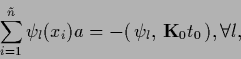 |
(303) |
the sum going over different 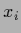 only.
Eq. (302) for
only.
Eq. (302) for 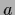 and
and 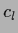 reads in data space,
similar to Eq. (271),
reads in data space,
similar to Eq. (271),
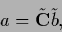 |
(304) |
where
 =
=
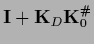 has been assumed invertible
and
has been assumed invertible
and 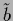 is given by the right hand side of Eq. (302).
Inserting into Eq. (301)
the solution finally can be written
is given by the right hand side of Eq. (302).
Inserting into Eq. (301)
the solution finally can be written
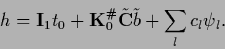 |
(305) |
Again, general non-quadratic data terms 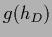 can be allowed.
In that case
can be allowed.
In that case
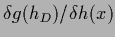 =
=
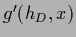 =
=
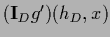 and Eq. (299)
becomes the nonlinear equation
and Eq. (299)
becomes the nonlinear equation
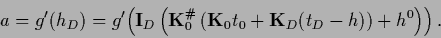 |
(306) |
The solution(s) 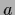 of that equation have then to be inserted
in Eq. (301).
of that equation have then to be inserted
in Eq. (301).




Next: Exact predictive density
Up: Regression
Previous: Regression
Contents
Joerg_Lemm
2001-01-21
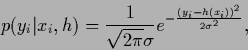
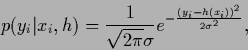
![]() measurement
of
measurement
of ![]() has to be understood as
measurement of a
has to be understood as
measurement of a
![]() =
=
![]() for sharply peaked
for sharply peaked ![]() .
We assume here that the discretization
of
.
We assume here that the discretization
of ![]() used in numerical calculations takes care of that averaging.
Divergent quantities like
used in numerical calculations takes care of that averaging.
Divergent quantities like ![]() -functionals,
used here for convenience, will then not be present.
-functionals,
used here for convenience, will then not be present.
![]() and define for training data
and define for training data ![]() ,
, ![]() the operator
the operator
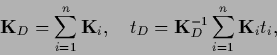
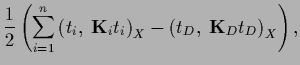
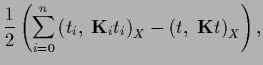
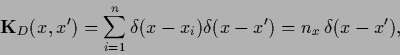
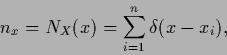
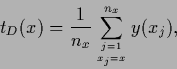
![]() :
Let us first study the case of an invertible
:
Let us first study the case of an invertible ![]() and consider the stationarity equation
as obtained from (248) or (250)
and consider the stationarity equation
as obtained from (248) or (250)
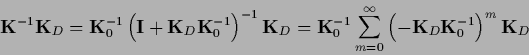
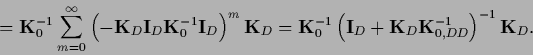
![]() is also known as equivalent kernel
due to its relation to kernel smoothing techniques
[210,94,90,76].
is also known as equivalent kernel
due to its relation to kernel smoothing techniques
[210,94,90,76].
![]() with any differentiable function
fulfilling
with any differentiable function
fulfilling
![]() =
= ![]() ,
where
,
where ![]() =
= ![]() is the restriction of
is the restriction of ![]() to data space.
Hence, also
the function of functional derivatives
with respect to
to data space.
Hence, also
the function of functional derivatives
with respect to ![]() is restricted to data space, i.e.,
is restricted to data space, i.e.,
![]() =
=
![]() with
with ![]() =
=
![]() and
and
![]() .
For example,
.
For example,
![]() =
=
![]() with
with ![]() a differentiable function.
The finite dimensional vector
a differentiable function.
The finite dimensional vector ![]() is then found by solving a nonlinear equation instead of a linear one
[73,75].
is then found by solving a nonlinear equation instead of a linear one
[73,75].
![]() ,
also
,
also ![]() , and thus
, and thus ![]() , is a vector for given
, is a vector for given ![]() .
(Considering the variable indicating the vector components of
.
(Considering the variable indicating the vector components of ![]() as part of the
as part of the ![]() -variable,
this is a situation where a fixed number of one-dimensional
-variable,
this is a situation where a fixed number of one-dimensional ![]() ,
corresponding to a subspace of
,
corresponding to a subspace of ![]() with fixed dimension,
is always measured simultaneously.)
In that case the diagonal
with fixed dimension,
is always measured simultaneously.)
In that case the diagonal ![]() of Eq. (246)
can be replaced by a version with non-zero off-diagonal elements
of Eq. (246)
can be replaced by a version with non-zero off-diagonal elements
![]() between the vector components
between the vector components ![]() of
of ![]() .
This corresponds
to a multi-dimensional Gaussian data generating probability
.
This corresponds
to a multi-dimensional Gaussian data generating probability
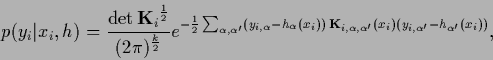
![]() :
For non-invertible
:
For non-invertible ![]() one can solve for
one can solve for ![]() using the Moore-Penrose inverse
using the Moore-Penrose inverse
![]() .
Let us first recall some basic facts
[58,164,186,187,126,15,120].
A pseudo inverse
.
Let us first recall some basic facts
[58,164,186,187,126,15,120].
A pseudo inverse ![]() of (a possibly non-square)
of (a possibly non-square) ![]() is defined by the conditions
is defined by the conditions
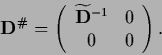
![]() there always exist orthogonal
there always exist orthogonal ![]() and
and ![]() so it can be written in orthogonal normal form
so it can be written in orthogonal normal form
![]() =
=
![]() ,
where
,
where ![]() is of the form of Eq. (287)
[120].
The corresponding Moore-Penrose inverse is
is of the form of Eq. (287)
[120].
The corresponding Moore-Penrose inverse is
![]() =
=
![]() .
.
![]() which can be diagonalized, i.e.,
for a square matrix
which can be diagonalized, i.e.,
for a square matrix ![]() =
=
![]() with diagonal
with diagonal ![]() ,
the Moore-Penrose inverse is
,
the Moore-Penrose inverse is
![]() =
=
![]() .
From Eq. (289) it follows then that
.
From Eq. (289) it follows then that
![]() is
diagonalizable because being positive semi-definite.
(In this case
is
diagonalizable because being positive semi-definite.
(In this case ![]() is an orthogonal matrix
and the entries of
is an orthogonal matrix
and the entries of ![]() are real and larger or equal to zero.)
Hence, one obtains under the condition
are real and larger or equal to zero.)
Hence, one obtains under the condition
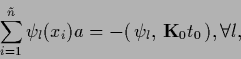
![]() can be allowed.
In that case
can be allowed.
In that case
![]() =
=
![]() =
=
![]() and Eq. (299)
becomes the nonlinear equation
and Eq. (299)
becomes the nonlinear equation