In classification
(or pattern recognition) tasks
the independent visible variable
![]() takes discrete values (group, cluster or pattern labels)
[16,61,24,47].
We write
takes discrete values (group, cluster or pattern labels)
[16,61,24,47].
We write
![]() =
= ![]() and
and
![]() =
= ![]() ,
i.e.,
,
i.e.,
![]() =
= ![]() .
Having received
classification data
.
Having received
classification data ![]() =
=
![]() the density estimation error functional
for a prior on function
the density estimation error functional
for a prior on function ![]() (with components
(with components ![]() and
and ![]() =
= ![]() )
reads
)
reads
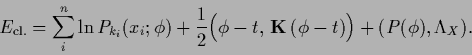 |
(335) |
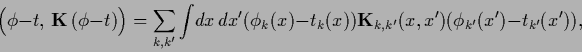 |
(336) |
For zero-one loss ![]() =
=
![]() -- a typical loss function for classification problems --
the optimal decision (or Bayes classifier) is given by the mode
of the predictive density
(see Section 2.2.2), i.e.,
-- a typical loss function for classification problems --
the optimal decision (or Bayes classifier) is given by the mode
of the predictive density
(see Section 2.2.2), i.e.,
| (337) |
For the choice ![]() non-negativity and normalization
must be ensured.
For
non-negativity and normalization
must be ensured.
For ![]() with
with ![]() non-negativity is automatically fulfilled
but the Lagrange multiplier must
be included to ensure normalization.
non-negativity is automatically fulfilled
but the Lagrange multiplier must
be included to ensure normalization.
Normalization is guaranteed by using
unnormalized probabilities
![]() ,
,
![]() (for which non-negativity has to be checked)
or
shifted log-likelihoods
(for which non-negativity has to be checked)
or
shifted log-likelihoods
![]() with
with
![]() , i.e.,
, i.e.,
![]() =
=
![]() .
In that case the nonlocal normalization terms are part of the likelihood
and no Lagrange multiplier has to be used
[236].
The resulting equation can be solved in the space defined by the
.
In that case the nonlocal normalization terms are part of the likelihood
and no Lagrange multiplier has to be used
[236].
The resulting equation can be solved in the space defined by the ![]() -data
(see Eq. (153)).
The restriction of
-data
(see Eq. (153)).
The restriction of ![]() =
= ![]() to linear functions
to linear functions
![]() yields log-linear models [154].
Recently a mean field theory for
Gaussian Process classification has been developed
[177,179].
yields log-linear models [154].
Recently a mean field theory for
Gaussian Process classification has been developed
[177,179].
Table 3 lists some special cases of density estimation. The last line of the table, referring to inverse quantum mechanics, will be discussed in the next section.