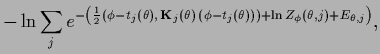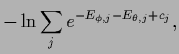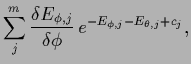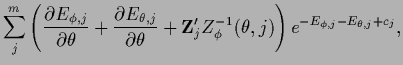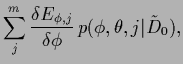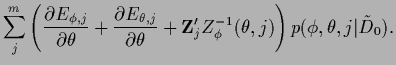Next: Prior mixtures for regression
Up: Non-Gaussian prior factors
Previous: Mixtures of Gaussian prior
Contents
Prior mixtures for density estimation
The mixture approach (535)
leads in general to non-convex error functionals.
For Gaussian components
Eq. (535) results in an error functional
where
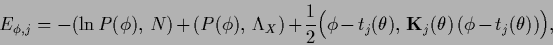 |
(538) |
and
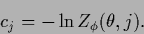 |
(539) |
The stationarity equations for 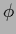 and
and 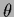
can also be written
Analogous equations are obtained
for parameterized 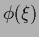 .
.




Next: Prior mixtures for regression
Up: Non-Gaussian prior factors
Previous: Mixtures of Gaussian prior
Contents
Joerg_Lemm
2001-01-21