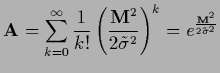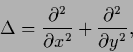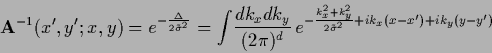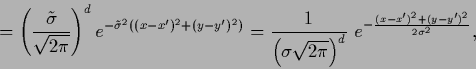Next: Inverting in subspaces
Up: Learning matrices
Previous: Massive relaxation
Contents
As Gaussian kernels are often used in density estimation and
also in function approximation
(e.g. for radial basis functions [191])
we consider the example
with positive semi-definite 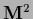 .
The contribution for
.
The contribution for 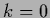 corresponds to a mass term
so for positive semi-definite
corresponds to a mass term
so for positive semi-definite 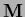 this
this 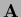 is positive definite and therefore invertible
with inverse
is positive definite and therefore invertible
with inverse
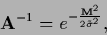 |
(655) |
which is diagonal and Gaussian in 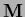 -representation.
In the limit
-representation.
In the limit
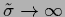 or for zero modes of
or for zero modes of 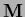 the Gaussian
the Gaussian
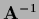 becomes the identity
becomes the identity 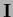 ,
corresponding to the gradient algorithm.
Consider
,
corresponding to the gradient algorithm.
Consider
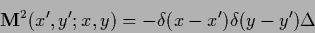 |
(656) |
where the 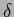 -functions
are usually skipped from the notation,
and
-functions
are usually skipped from the notation,
and
denotes the Laplacian.
The kernel of the inverse is diagonal in Fourier representation
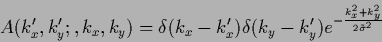 |
(657) |
and non-diagonal, but also Gaussian in 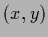 -representation
-representation
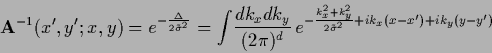 |
(658) |
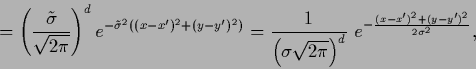 |
(659) |
with
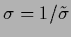 and
and 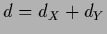 ,
, 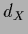 = dim(
= dim(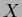 ),
), 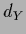 = dim(
= dim(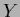 ).
).




Next: Inverting in subspaces
Up: Learning matrices
Previous: Massive relaxation
Contents
Joerg_Lemm
2001-01-21