Next: Bibliography
FUZZY RULES AND REGULARIZATION THEORY
Jörg C. Lemm
Institut für Theoretische Physik I
Wilhelm-Klemm-Str.9, D-48149 Münster, Germany
Tel. (+49)251/83-34922
Fax (+49)251/83-36328
lemm@uni-muenster.de
ABSTRACT:
Regularization theory and
stochastic processes have the advantage
that a-priori information is expressed directly
in terms of the function values of interest.
Classical regularization functionals are convex
and possess a unique minimum.
On the other hand,
convex functionals can only implement AND-like
combinations of approximation conditions.
The paper discusses
the empirical measurement of general, also non-convex a-priori information
and its technical implementation
by fuzzy logical-like combinations
of quadratic building blocks.
1. INTRODUCTION
The generalization ability of empirical learning systems
is essentially based on dependencies between
known training data and future test situations.
Those dependencies are part of the a-priori information
necessary for any empirical learning.
We discuss in this paper aspects
of the empirical
measurement or control of a-priori information.
We concentrate on the regularization approach
(Tikhonov, 1963).
Given training data
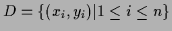 we aim in finding an approximation or hypothesis function
we aim in finding an approximation or hypothesis function
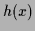 which minimizes a given error functional
which minimizes a given error functional 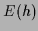 .
A typical functional
.
A typical functional
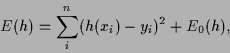 |
(1) |
consists of two terms,
a mean-square training error and an additional prior term.
A possible smoothness related prior term is
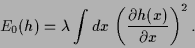 |
(2) |
In regularization theory prior terms,
and hence the dependencies between training and test data,
are directly formulated
in terms of the function values 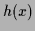 .
Often this is much easier to interpret than dependencies
which are implicit in a chosen parameterization of
.
Often this is much easier to interpret than dependencies
which are implicit in a chosen parameterization of 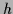 (for example as neural network)
or in a chosen algorithm
(for example with specific initial conditions or stopping rule).
From a Bayesian point of view regularization theory has an interpretation
in terms of stochastic processes (Doob, 1953, Wahba, 1990)
or stochastic fields
like they appear in statistical mechanics
or statistical field theory (Itzykson & Drouffe, 1989).
Classical regularization approaches
include for example Radial Basis Functions approaches
and various spline
methods(Poggio & Girosi, 1990, Girosi, Jones, & Poggio, 1995).
(for example as neural network)
or in a chosen algorithm
(for example with specific initial conditions or stopping rule).
From a Bayesian point of view regularization theory has an interpretation
in terms of stochastic processes (Doob, 1953, Wahba, 1990)
or stochastic fields
like they appear in statistical mechanics
or statistical field theory (Itzykson & Drouffe, 1989).
Classical regularization approaches
include for example Radial Basis Functions approaches
and various spline
methods(Poggio & Girosi, 1990, Girosi, Jones, & Poggio, 1995).
In Section 2 we discuss aspects of empirical control
of prior knowledge.
Section 3 shows non-convex functionals obtained by fuzzy-like methods.
2. EMPIRICAL MEASUREMENT OF A-PRIORI INFORMATION
The crucial role of the dependencies between training data and test data
for generalization would in principle require
strict empirical control of these dependencies.
Such an empirical control or measurement of a-priori information
is of special practical importance in low data scenarios
or when security aspects require to control the response
to all potential test situations.
Three reasons may be mainly responsible for
the lack of empirical measurement of a-priori information
in practice:
- 1.
- A-priori information corresponds to
an infinite number of data.
Empirical measurement of a-priori information
requires data for every potential test situation
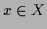 .
For infinite or even continuous
.
For infinite or even continuous 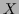 this corresponds to
an infinite amount of data.
A simple example are bounds
like
this corresponds to
an infinite amount of data.
A simple example are bounds
like 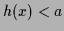 ,
,
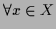 .
The practical problem is:
How can an infinite number of data be measured in practice?
.
The practical problem is:
How can an infinite number of data be measured in practice?
- 2.
- A-priori information is often complex, unsharp, and non-convex.
The dependency structure may be very complicated.
For example, a class of objects, like
faces, cars, phonemes, pedestrians, characters,
 ,
is never well defined by the available training examples alone.
It is implicitly defined by the selection process
of training examples,
often done by human experts.
Hence, mostly only qualitative, e.g. verbal, information will be available.
Prior knowledge enumerating
alternative possibilities has a non-convex structure.
For example, one may expect an eye to be open OR closed,
or a photo to show either the seashore OR
mountains.
Such OR-like combinations yield
regularization functionals with multiple minima
and non-linear stationarity equations.
,
is never well defined by the available training examples alone.
It is implicitly defined by the selection process
of training examples,
often done by human experts.
Hence, mostly only qualitative, e.g. verbal, information will be available.
Prior knowledge enumerating
alternative possibilities has a non-convex structure.
For example, one may expect an eye to be open OR closed,
or a photo to show either the seashore OR
mountains.
Such OR-like combinations yield
regularization functionals with multiple minima
and non-linear stationarity equations.
- 3.
- Explicit implementation of prior knowlegde is computationally costly.
Typically, parameterized function spaces,
e.g. neural networks,
contain dependencies
which are difficult to analyze and to control by humans.
To avoid
implicit restrictions introduced by parameterizations
one has to treat the single function values
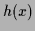 itself
as primary degrees of freedom.
Such approaches, like
regularization theory, stochastic processes
or statistical field theory in physics
require usually large computational resources.
itself
as primary degrees of freedom.
Such approaches, like
regularization theory, stochastic processes
or statistical field theory in physics
require usually large computational resources.
The problems can be attacked at least partly.
- 1.
- A-priori information can be measured by a-posteriori
control.
Bounds for an infinite number of function values, for example,
can simply be ensured by using measurement devices with
a cut-off function.
Analogously, exact or approximate symmetries,
like smoothness for infinitesimal translations,
can be realized by input noise or input averaging
with respect to the symmetry group under consideration
(Bishop, 1995, Leen, 1995, and Lemm, 1996).
The key point is that even for
a formally infinite number of potential test situations
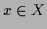 only a finite number of
only a finite number of 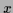 actually appears as test situation.
Hence, a-priori information
corresponding to an infinite number of data
must be enforced by a-posteriori control
of application situation.
actually appears as test situation.
Hence, a-priori information
corresponding to an infinite number of data
must be enforced by a-posteriori control
of application situation.
- 2.
- Unsharp prior knowledge
can be quantified using fuzzy techniques.
As most practical important functions or object classes
are not sufficiently well defined by training examples alone,
but by training example selecting and performance evaluating
human experts, there is a clear need
in quantifying unsharp, verbally formulated knowledge.
(See for example Klir & Yuan, 1995, 1996.)
For example,
verbal descriptions of faces can be used to construct quantitative
templates for prototypical forms of
constituents (e.g. eyes, nose, mouth),
their variants (e.g. open vs. closed mouth,
translated, scaled, or deformed eyes)
and relations (e.g. typical spatial distances).
Defining
AND and OR-like combinations of constituent templates
the image of a face,
incomplete and disturbed by noise, may be reconstructed
by approximating given
noisy data points of the
incomplete image AND typical templates of constituents
AND their spatial relations in either one of their variants,
for example, a template for open OR for closed eyes.
- 3.
- Increasing computational resources allow
the use of more costly numerical methods.
Especially low dimensional problems are suited
for adaption of methods of
statistical mechanics or lattice field theory(Montvay & Muenster, 1994).
Typical examples are Monte-Carlo methods
used for one-dimensional time series
or two-dimensional image reconstruction tasks
(Zhu & Mumford,1997).
3. NON-CONVEX FUNCTIONALS
We choose
quadratic building blocks
to construct arbitrary complex
prior functionals.
Classical regularization functionals like (1)
consist of a sum of quadratic terms.
Indeed, we may write for (2)
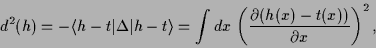 |
(3) |
where 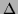 denotes the
Laplacian
denotes the
Laplacian
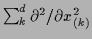 (for
(for 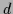 -dimensional
-dimensional 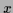 )
and we used partial integration assuming vanishing boundary terms
and angular brackets to denote the matrix elements of
a symmetric operator. In (3) a ``template function''
)
and we used partial integration assuming vanishing boundary terms
and angular brackets to denote the matrix elements of
a symmetric operator. In (3) a ``template function'' 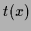 has been introduced.
This function
has been introduced.
This function 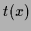 is identically zero in (2)
but comparing with a mean-square training error term
is identically zero in (2)
but comparing with a mean-square training error term
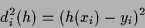 |
(4) |
we see that 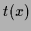 in (3) generalizes
discrete training data to continuous data.
Such continuous data functions are always present
in quadratic prior terms but can be chosen identically zero
in functionals of form (1),
where only one quadratic prior term is present,
by solving for
in (3) generalizes
discrete training data to continuous data.
Such continuous data functions are always present
in quadratic prior terms but can be chosen identically zero
in functionals of form (1),
where only one quadratic prior term is present,
by solving for 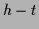 instead for
instead for 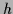 .
For functionals with
more than one prior term not all template functions can be set to zero
at the same time.
Hence, we include explicitly continuous data functions
.
For functionals with
more than one prior term not all template functions can be set to zero
at the same time.
Hence, we include explicitly continuous data functions 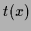 and use as fundamental building blocks
``quadratic concepts'' of the form
and use as fundamental building blocks
``quadratic concepts'' of the form
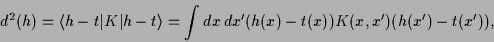 |
(5) |
where 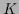 is a positive definite real symmetric
matrix or operator, so
is a positive definite real symmetric
matrix or operator, so 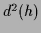 represents a square distance.
Quadratic concepts encompass the
mean-square error as well as classical prior terms
and correspond to
a Gaussian process
represents a square distance.
Quadratic concepts encompass the
mean-square error as well as classical prior terms
and correspond to
a Gaussian process
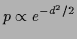 with covariance
with covariance 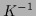 .
.
A sum of terms as in (1)
implements an AND in probabilistic interpretation,
i.e., functional (1) requires
training data AND prior term to be approximated.
A probabilistic OR can be implemented by a mixture model.
In the case of two alternative concepts 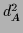 and
and 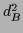 with equal
with equal 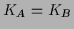 in addition to standard training data
in addition to standard training data 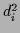 one can minimize
one can minimize
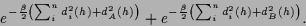 |
(6) |
Here 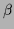 is a technically useful
convexity parameter
also known as inverse temperature
(Rose, Gurewitz, & Fox, 1990, Yuille & Kosowski, 1994).
Non-zero template functions
is a technically useful
convexity parameter
also known as inverse temperature
(Rose, Gurewitz, & Fox, 1990, Yuille & Kosowski, 1994).
Non-zero template functions 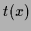 yield inhomogeneous stationarity equations
which are, for example, similar
to equations appearing in quantum mechanical scattering theory (Lemm, 1995).
Alternatively,
a product implementation of OR for square distances
yields
yield inhomogeneous stationarity equations
which are, for example, similar
to equations appearing in quantum mechanical scattering theory (Lemm, 1995).
Alternatively,
a product implementation of OR for square distances
yields
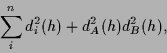 |
(7) |
resembling the Landau-Ginzburg treatment of phase transitions
in statistical mechanics.
For technical details see (Lemm, 1996).
4. CONCLUSIONS
The paper emphasizes
the possibility of empirical measurement or control of a-priori information
corresponding to an infinite number of data.
Methods have been presented implementing complex prior knowledge
by combinations of quadratic building blocks.
OR-like combinations resulting
in non-convex regularization functionals require methods
going beyond classical quadratic regularization
or Gaussian process approaches.
ACKNOWLEDGEMENTS
The author was supported by a Postdoctoral Fellowship (Le 1014/1-1)
from the Deutsche Forschungsgemeinschaft and a NSF/CISE Postdoctoral
Fellowship at the Massachusetts Institute of Technology.
He also wants to thank
Federico Girosi and Tomaso Poggio for stimulating discussions.



Next: Bibliography
Joerg_Lemm
2000-09-22
![]() we aim in finding an approximation or hypothesis function
we aim in finding an approximation or hypothesis function
![]() which minimizes a given error functional
which minimizes a given error functional ![]() .
A typical functional
.
A typical functional
![]() and
and ![]() with equal
with equal ![]() in addition to standard training data
in addition to standard training data ![]() one can minimize
one can minimize