[@twocolumnfalse

Published in Phys. Rev. Lett. 84 (2000), 2068

A Bayesian Approach to Inverse Quantum Statistics

J. C. Lemm, J. Uhlig, and A. Weiguny

September 12, 2000

Institut für Theoretische Physik I, Universität Münster, 48149 Münster, Germany

Abstract:

A nonparametric Bayesian approach is developed to determine quantum potentials from empirical data for quantum systems at finite temperature. The approach combines the likelihood model of quantum mechanics with a priori information on potentials implemented in form of stochastic processes. Its specific advantages are the possibilities to deal with heterogeneous data and to express a priori information explicitly in terms of the potential of interest. A numerical solution in maximum a posteriori approximation is obtained for one-dimensional problems. The number of measurements being small compared to the degrees of freedom of a nonparametric estimate, the results depend strongly on the implemented a priori information.

05.30.-d, 02.50.Rj, 02.50.Wp ]

The last decade has seen a rapidly growing interest in learning from empirical data. Increasing computational resources enabled successful applications of empirical learning algorithms in many different areas including, for example, time series prediction, image reconstruction, speech recognition, and many more regression, classification, and density estimation problems. Empirical learning, i.e., the problem of finding underlying general laws from observations, represents a typical inverse problem and is usually ill-posed in the sense of Hadamard [1,2,3]. It is well known that a successful solution of such problems requires additional a priori information. In empirical learning it is a priori information which controls the generalization ability of a learning system by providing the link between available empirical ``training'' data and unknown outcome in future ``test'' situations.

The empirical learning problem we study in this Letter is the reconstruction of potentials from measuring quantum systems at finite temperature, i.e., the problem of inverse quantum statistics. Two classical research fields dealing with the determination of potentials are inverse scattering theory [4] and inverse spectral theory [5,6]. They characterize the kind of data which are necessary, in addition to a given spectrum, to identify a potential uniquely. For example, such data can be a second complete spectrum for different boundary conditions, knowledge of the potential on a half interval, or the phase shifts as a function of energy. However, neither a complete spectrum nor specific values of potentials or phase shifts for all energies can be determined empirically by a finite number of measurements. Hence, any practical algorithm for reconstructing potentials from data must rely on additional a priori assumptions, if not explicitly then implicitly. Furthermore, besides energy, other observables like particle coordinates or momenta may have been measured for a quantum system. Therefore, the approach we study in this Letter is designed to deal with arbitrary data and to treat situation specific a priori information in a flexible and explicit manner.

Many disciplines have contributed empirical learning algorithms, some of the most widely spread being decision trees, neural networks, projection pursuit techniques, various spline methods, regularization approaches, graphical models, support vector machines, and, becoming especially popular recently, nonparametric Bayesian methods [2,7,8,9,10,11]. Motivated by the clear and general framework it provides, the approach we will rely on is that of Bayesian statistics [12,13] which can easily be adapted to inverse quantum statistics. Computationally, however, its application to quantum systems turns out to be more demanding than, for example, typical applications to regression problems.

A Bayesian approach is based on two probability densities: 1. a likelihood model $p(x\vert O,v)$, quantifying the probability of outcome $x$ when measuring observable $O$ given a (not directly observable) potential $v$ and 2. a prior density $p_0(v)$ = $p(v\vert D_0)$ defined over a space ${\cal V}$ of possible potentials assuming a priori information $D_0$. Further, let $D_T$ = $(x_T,O_T)$ = $\{(x_i,O_i)\vert 1\le i\le n\}$ denote available training data and $D$ = $D_T \cup D_0$ the union of training data and a priori information. To make predictions we aim at calculating the predictive density for given data $D$

$$p(x\vert O,D) = \int \!dv\, p(x\vert O,v)\, p(v\vert D),$$ (1)

assuming $p(x\vert O,v,D)$ = $p(x\vert O,v)$, $p(v\vert O,D)$ = $p(v\vert D)$. The posterior density $p(v\vert D)$ appearing in that formula is related to prior density and likelihood through Bayes' theorem $p(v\vert D)$ = $p(x_T\vert O_T,v)\,p_0(v)/p_0(x_T\vert O_T)$, where the likelihood factorizes for independent data $p(x_T\vert O_T,v)$ = $\prod_i p(x_i\vert O_i,v)$ and the denominator is $v$-independent. The $v$-integral stands for an integral over parameters if we choose a parameterized space ${\cal V}$, or for a functional integration if ${\cal V}$ is an infinite dimensional function space. Because we will in most cases not be able to solve that integral exactly we treat it in maximum a posteriori approximation, i.e., in saddle point approximation if the likelihood varies slowly at the stationary point. Then, assuming $p(x\vert O,D) \approx p(x\vert O,v^*)$ with $v^*$ = ${\rm argmax}_{v\in{\cal V}} p(v\vert D)$, integration is replaced by maximization.

According to the axioms of quantum mechanics, observables $O$ are represented by hermitian operators and the probability of finding outcome $x$ measuring observable $O$ is given by

$$p(x\vert O,v) = {\rm Tr} \Big(P_O(x) \, \rho(v) \Big) .$$ (2)

Here $\rho$ denotes the density operator of the quantum mechanical system and $P_O(x)$ = $\sum_\xi \vert x,\xi \!\!><\!\!x,\xi \vert$ is the projector on the space spanned by the orthonormalized eigenfunctions $\vert x,\xi\!\!>$ of $O$ with eigenvalue $x$. The label $\xi$ distinguishes eigenfunctions which are degenerate with respect to $O$. If the system is not in an eigenstate of the observable $O$, a quantum mechanical measurement changes the state of the system. Hence, to perform repeated measurements under the same $\rho$ requires the restoration of $\rho$ before each measurement.

In particular, we will consider a canonical ensemble of quantum systems at temperature $1/\beta$ (setting Boltzmann's constant to 1) characterized by the density operator $\rho$ = $\exp (-\beta H)/({\rm Tr\,} \exp(-\beta H))$. Furthermore, we assume a Hamiltonian $H$ = $T + V$ being the sum of a kinetic energy term $T$ for a particle with mass $m$ and an unknown local potential $V(x,x^\prime)$ = $v(x) \delta (x-x^\prime )$ which we want to reconstruct from data. In case of repeated measurements in a canonical ensemble one has to wait with the next measurement until thermal equilibrium is reached again. We will in the following focus on measurements of particle coordinates in a single particle system in a heat bath with temperature $1/\beta$. In that case the $x_i$ represent particle positions corresponding to measurements of the observable $O_i$ = $\hat x$ with $\hat x \vert x_i\!\!>$ = $x_i\vert x_i\!\!>$. The likelihood becomes

$$p(x_i\vert\hat x,v) =\sum_\alpha p_\alpha \vert\phi_\alpha(x_i)\vert^2 =<\vert\phi (x_i)\vert^2> ,$$ (3)

for $H\vert\phi_\alpha\!\!>$ = $E_\alpha \vert\phi_\alpha\!\!>$ and with $<\!\!\cdots\!\!>$ denoting a thermal expectation value with probabilities $p_\alpha$ = $\exp(-\beta E_\alpha)/Z$ and $Z$ = $\sum_\alpha \exp (-\beta E_\alpha)$. One may also add a classical noise process $p(\bar x_i\vert x_i)$ on top of $x_i$ in which case an additional integration is necessary to get the density $p(\bar x_i\vert\hat x,v)$ = $\int \! dx_i \, p(\bar x_i\vert x_i) \, p(x_i\vert\hat x,v)$ of the noisy output $\bar x_i$.

Already at zero temperature, even complete knowledge of the true likelihood would just determine the modulus of the ground state and thus not be sufficient to determine a potential uniquely. The situation is still worse in practice, where only a finite number of probabilistic measurements is available, and at finite temperatures, as the likelihood becomes uniform in the infinite temperature limit. Hence, in addition to Eq.(2) giving the likelihood model of quantum mechanics, it is essential to include a prior density over a space of possible potentials $v$. To be able to formulate a priori information explicitly in terms of the function values $v(x)$ we use a stochastic process. Technically convenient is a Gaussian process prior density

$$p_0(v) = \left(\det \frac{\lambda {\bf K}_0}{2\pi}\right)^\... ...} e^{-\frac{\lambda}{2}<v-v_0 \vert {\bf K}_0 \vert v-v_0 >} ,$$ (4)

with mean $v_0$, representing a reference potential or template for $v$, and a real symmetric, positive (semi-)definite covariance operator $(\lambda{\bf K}_0)^{-1}$, acting on potentials $v$ rather than on wave functions and measuring the distance between $v$ and $v_0$. Here $\lambda$ is technically equivalent to a Tikhonov regularization parameter. If allowed to vary, $\lambda$ is an example of a so called hyperparameter, parameterizing the prior density. Such parameters have to be included in the integration of Eq.(1) and are often also treated in maximum a posteriori approximation.

Typical choices for ${\bf K}_0$ implementing smoothness priors are the negative Laplacian ${\bf K}_0$ = $-\Delta$, e.g., in one dimension $-\Delta$ = $-d^2/dx^2$, or a Radial Basis Function prior ${\bf K}_0$ = $\exp{(-{\sigma_{\rm RBF}^2}{\Delta}/2)}$ [14]. Gaussian process priors can, for example, be related to approximate symmetries. Assume we expect the potential to commute approximately with a unitary symmetry operation $S$. Then $V \approx S^\dagger V S$ = ${\bf S} V$ defines an operator ${\bf S}$ acting on potentials $V$. In that case a natural prior would be $p_0\propto\exp (-E_{S})$ with $E_S$ = $<\!V-{\bf S}V\vert V-{\bf S}V\!>\!\!\!/2$ = $<\! V \vert{\bf K}_{0}\vert V\!>\!\!\!/2$ for ${\bf K}_0$ = $({\bf I}-{\bf S})^\dagger ({\bf I}-{\bf S})$ and ${\bf I}$ denoting the identity. Note that symmetric potentials are in the null space of such a ${\bf K}_0$, hence another prior has to be included unless the combination with training data does determine the potential. Similarly, for a Lie group ${\bf S}(\theta)$ = $\exp (\theta {\bf s})$ an approximate infinitesimal symmetry is implemented by ${\bf K}_0$ = ${\bf s}^\dagger{\bf s}$. In particular, a negative Laplacian smoothness prior enforces approximate symmetry under infinitesimal translation. Alternatively, a more explicit prior implementing an approximate symmetry can be obtained by choosing a symmetric reference potential $V_0$ = $S^\dagger V_0 S$ and $E_S$ = $<\!V-V_0\vert V-V_0\!>\!/2$.

While a Gaussian process prior is only able to model a unimodal, concave prior density, more general prior densities can be arbitrarily well approximated by mixtures of Gaussian process priors [15]

$$p_0(v) =\sum_{k=1}^M p_0(k) \,p_0(v\vert k),$$ (5)

with mixture probabilities $p_0(k)$ and Gaussian prior processes $p_0(v\vert k)$ having means $v_k$ and covariances $(\lambda {\bf K}_k)^{-1}$.

To find the potential with maximal posterior we maximize for independent data, following Bayes' theorem,

$$p(v\vert D) \propto p_0(v) \prod_{i=1}^n p(x_i\vert O_i,v) .$$ (6)

This is done by requiring the functional derivatives of the log-posterior (technically often more convenient than the posterior) with respect to $v(x)$ to be zero,

$$\delta_{v(x)} \ln p(v\vert D) = 0$$ (7)

where $\delta_{v(x)}$ stands for $\delta/\left(\delta v(x)\right)$. To calculate the functional derivative of the likelihoods in Eq.(6) we need $\delta_{v(x)} E_\alpha$ as well as $\delta_{v(x)} \phi_\alpha(x^{\prime})$. These quantities can be found by taking the functional derivative of the eigenvalue equation of the Hamiltonian yielding, for orthonormal, nondegenerate eigenfunctions,

$$\delta_{v(x)} E_\alpha = <\!\!\phi_\alpha \vert\, \delta_{v(x)} H \,\vert \phi_\alpha\!\!> =\vert\phi_\alpha(x)\vert^2 ,$$ (8)

$$\delta_{v(x)} \phi_\alpha(x^{\prime}) = \sum_{\gamma\ne \alpha} \frac{1}{E_\alpha-E_\gamma} \phi_\gamma(x^{\prime})\phi^*_\gamma(x) \phi_\alpha (x) ,$$ (9)

using $\delta_{v(x)} H (x^\prime,x^{\prime\prime})$ = $\delta_{v(x)} V (x^\prime,x^{\prime\prime})$ = $\delta(x-x^\prime) \delta (x^\prime-x^{\prime\prime})$ and taking $<\!\phi_\alpha\vert\delta_{v(x)}\phi_\alpha\!>$ = 0. Now it is straightforward to calculate the functional derivative of the likelihood

$$\delta_{v(x)}p(x_i\vert\hat x,v) =$$ (10)

$$\quad <\left(\delta_{v(x)}\phi^*(x_i)\right) \phi (x_i)> +<\phi^*(x_i)\delta_{v(x)}\phi (x_i)>$$

$$- \beta \left( < \vert\phi (x_i)\vert^2 \vert\phi (x)\vert^2 > -< \vert\phi (x_i)\vert^2>< \vert\phi (x)\vert^2> \right) .$$

Finally, using

$$\delta_{v(x)} \ln p_0 = -\lambda{\bf K}_0(v-v_0) ,$$ (11)

the functional derivative of the posterior can be calculated. Formula (11) is also valid for Gaussian mixture models of the form (5) provided we understand ${\bf K}_0$ = $\sum_k p_0(k\vert v)\,{\bf K}_k$ and $v_0$ = ${\bf K}_0^{-1} \sum_k p_0(k\vert v)\, {\bf K}_k v_k$ where $p_0(k\vert v)$ = ${p_0(v\vert k)p_0(k)}/{p_0(v)}$.

It is straightforward to include also other kinds of data or a priori information. For example, a Gaussian smoothness prior as in Eq.(4) with zero reference potential $v_0\equiv 0$ and $v(x)$ = 0 at the boundaries tends to lead to flat potentials when the regularization parameters $\lambda$ becomes large. For such cases it is useful to include besides smoothness also a priori information or data which are related more directly to the depth of the potential. One such possibility is to include information about the average energy $U$ = $<\!E\!>$ = $\sum_\alpha p_\alpha E_\alpha$. The average energy can then be controled by introducing a Lagrange multiplier term $\mu (U - \kappa)$, or, technically sometimes easier, by a term representing noisy energy data $\kappa$,

$$p_U \propto e^{-E_U} ,\quad E_U = \frac{\mu}{2} (U - \kappa)^2,$$ (12)

so that $U\rightarrow\kappa$ for $\mu\rightarrow\infty$. Using $\delta_{v(x)} U$ = $<\!\delta_{v(x)} E\!>-\beta <\!E\; \delta_{v(x)} E\!>$ + $\beta <\!E\!> <\!\delta_{v(x)} E\!>$, we find for the functional derivative of $E_U$

$$\delta_{v(x)} E_U = \mu\left(U\!-\!\kappa\right) <\! \vert... ...\vert^2 \left( 1-\beta \left( E \; -U \right) \right) \!> .$$ (13)

Collecting all terms we are now able to solve the stationarity Eq.(7) by iteration. Starting with an initial guess $v^{(0)}$, choosing a step width $\eta$ and a positive definite matrix ${\bf A}$ we can iterate according to

$$v^{(r+1)} = v^{(r)}\! + \eta {\bf A}^{-1} \Big( {\bf K}_0^{(r)} (v_0\!-\!v^{(r)})$$ (14)

$$+\sum_i \delta_{v(x)}\ln p(x_i\vert\hat x,v^{(r)}) -\delta_{v(x)} E_U^{(r)} \Big) .$$

Here we included an $E_U$ term which depends on $v$, like ${\bf K}_0$ for mixture models, and thus changes during iteration. Typically, $\eta$ and often also ${\bf A}$ are adapted during iteration. In the numerical examples we have studied, ${\bf A}$ = $\lambda {\bf K}_0$ proved to be a good choice. Note that in general different initial guesses $v^{(0)}$ can yield different solutions.

The numerical difficulties of the nonparametric Bayesian approach arise from the fact that the quantum mechanical likelihood (2) is non-Gaussian and non-local in the potential $v(x)$. Similar to general density estimation problems, even for Gaussian priors none of the $v(x)$-integrations in (1) can be carried out analytically [16]. In contrast, for example, Gaussian regression problems have a likelihood being Gaussian and local in the function of interest, and an analogous nonparametric Bayesian approach with a Gaussian process prior requires only to deal with matrices with dimension not larger than the number of training data [11]. The following examples will show, however, that a direct numerical solution of Eq.(7) by discretization is feasible for one-dimensional problems. Higher dimensional problems, on the other hand, require further approximations. For example, work on inverse many-body problems on the basis of a Hartree-Fock approximation is in progress.

Figure 1: Reconstruction of an approximately periodic potential from coordinate measurements. Shown are (a) empirical density, i.e., relative frequencies of sampled data (bars), true (thin line) and reconstructed likelihood (thick line) (b) $v_{\rm true}$ (thin line), reference potential $v_0$ = $\sin(\pi x/3)$ (dashed), and reconstructed potential $v$ (thick line). (200 data points, mesh with 30 points, $m$ = 0.25 for $\hbar$ = 1, $\beta$ = 4, ${\bf K}_0$ = $-\Delta$, $\lambda$ = 0.2, $\mu$ = 0, $U (v_{\rm true})$ = $-0.354$, $U(v)$ = $-0.552$.)

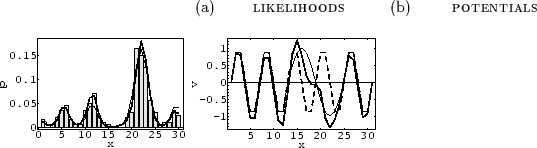In the following numerical examples we discuss the reconstruction of an approximately periodic, one-dimensional potential $v$, with the reference potential $v_0$ chosen periodic. The potential $v$ may describe a one-dimensional surface, deviating from exact periodicity due to localized defects. To enforce the deviation from $v_0$ to be smooth we take as prior on $v$ a negative Laplacian covariance, i.e., ${\bf K}_0$ = $-\Delta$. Fig.1 shows representative numerical results for a grid with 30 points and 200 data sampled from the likelihood $p(x\vert\hat x,v_{\rm true})$ for some chosen potential $v_{\rm true}$. The reconstructed potential $v$ has been found by iterating without energy penalty term $E_U$ according to Eq.(14) with ${\bf A}$ = ${\bf K}_0$. We took zero boundary conditions for $v$, so ${\bf K}_0$ becomes invertible, and, consistently, periodic boundary conditions for the eigenfunctions $\phi_\alpha$. Note that the data have been sufficient to identify clearly the deviation from the periodic reference potential. Fig.2a shows the same example with an energy penalty term $E_U$ with $\kappa$ = $U (v_{\rm true})$. While the reconstructed likelihood (not shown) is not much altered, the true potential is now better approximated in regions where it is small. As a rule, similar likelihoods do not necessarily imply similar potentials, and vice versa.

Figure 2: Reconstruction with energy penalty term $E_U$ with $\kappa$ = $U (v_{\rm true})$ = $-0.354$. Shown are true (thin lines), reconstructed (thick lines), and reference potential (dashed). (a) ${\bf K}_0$ = $-\Delta$, $v_0(x)$ = $\sin(\pi x/3)$, $\mu$ = 1000, $U(v)$ = $-0.353$. (b) ${\bf K}_0$ = $-\Delta -\gamma \Delta _\theta$, $v_0\equiv 0$, $\theta$ = 6, $\gamma$ = 0.12, $\lambda$ = 0.05, $\mu$ = 10, $U(v)$ = $-0.351$. All other parameters as for Fig.1.

Figure 3: Reconstruction of symmetric potential with mixture of Gaussian priors. (a) shows empirical density (bars), true (thin line) and reconstructed likelihood (thick line). (b) shows the true potential (thin line), the two reference potentials $v_1$ and $v_2$ (dashed lines), and a solution for the reconstructed potential $v$ (thick line). Because both reference potentials are partially supported by the data the approximated $v$ is a mixture of the solutions for $v_1$ and $v_2$. (Final mixture coefficients $p_0(1\vert v)$ = 0.57, $p_0(2\vert v)$ = 0.43, 20 data points, mesh with 31 points, $v(x)$ = $v(-x)$, boundary condition $v(\pm 15)$ = 0, and $m$ = 0.1, $\beta$ = 1, ${\bf K}_0$ = $-\Delta$, $\lambda$ = 0.5, $\mu$ = 10, $\kappa$ = $-10,01$ = $U (v_{\rm true})$ resulting in $U(v)$ = $-10.1$.)

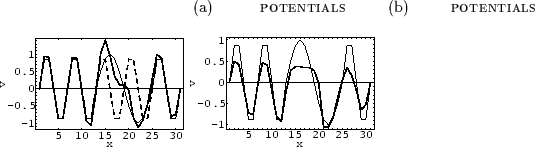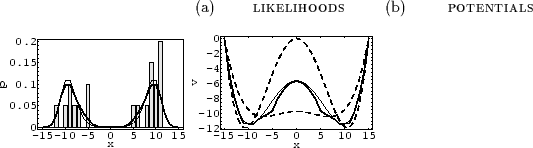Fig.2b shows the implementation of approximate periodicity by an operator $\Delta_\theta$, defined by $<\!\!v\vert\Delta_\theta \vert v\!\!>$ = $\int \!dx \vert v(x)-v(x+\theta)\vert^2$ for periodic boundary conditions on $v$, thus measuring the difference between the potential $v(x)$ and the potential translated by $\theta$. To find smooth solutions we added a negative Laplacian term with zero reference potential, i.e., we used ${\bf K}_0$ = $-\Delta -\gamma \Delta _\theta$. To have an invertible matrix for periodic boundary conditions on $v$ we iterated this time with ${\bf A}$ = ${\bf K}_0$ + $0.1 {\bf I}$. The implementation of approximate periodicity by $\Delta_\theta$ instead of a periodic $v_0$ is more general in so far as it annihilates arbitrary functions with period $\theta$. As, however, the reference function of the Laplacian term does not fit the true potential very well, the reconstruction is poorer in regions where the potential is large and thus no data are available. In these regions a priori information is of special importance. Finally, Fig.3 shows the implementation of a mixture of Gaussian prior processes.

In conclusion, we have applied a nonparametric Bayesian approach to inverse quantum statistics and shown its numerical feasibility for one-dimensional examples.