
You pull a piece of paper out of your pocket with the result written on it: 6174.
Answer: 2.71828… = e, Euler's number
Question: Are there irrational numbers a and b for which the power ab is rational?
Amazingly, there is an elementary proof that such numbers exist:

Curiously, there was doubt for a while: in 1853, William Shanks published the result of his years-long calculation of 607 decimal places of π, which he later expanded to 707 places. Augustus De Morgan noticed that among the 607 digits, the number 7 only appears 44 times. The deviation from the most likely number 61 is significantly larger than one would statistically expect, and the suspicion arose that the numbers are not evenly distributed.
It was only in 1946 that D. Ferguson discovered that Shanks had made a mistake and only the first 527 digits were correct. As things stand today, π seems to be "normal".
By the way, if it is so, every finite sequence of digits would appear somewhere in it; e.g. the sequence 31415926 occurs first at the 50366472nd place after the decimal point. You can search for your birthday or other sequences on the Pi-Search Page.
The optimal strategy goes like this: You look at the proportion x (0 < x <1) of the houses. Then choose the first house that you like better than all the previous ones.
The strategy is optimal for the choice
x = 1/e ~ 0.37
Of course there is no guarantee that you will get the best house for you; if you are unlucky it could even be the worst, but for x = 1/e you are most likely to get the best house for you.
Popular is 22/7 = 3.1428... Noteworthy is the fraction 355/113 = 3.14159292..., which was discovered by the Chinese mathematician Zu Chongzhi in the 5th century, and which is easy to remember (113355). This approximation is very efficient, because it represents 7 digits of π (including the 3) using 6 digits. Are there any more efficient rational approximations?
As a measure of efficiency, let's consider the number of correct digits divided by the number of digits required. Mathematically formulated a bit better is the ratio R = - log(|π - p/q|) / log(pq).
For 22/7, R = 1.325, and for 355/113, R = 1.428.
Can it get any more efficient?
The best rational approximations for irrational numbers are provided by regular continued fractions. For π it is
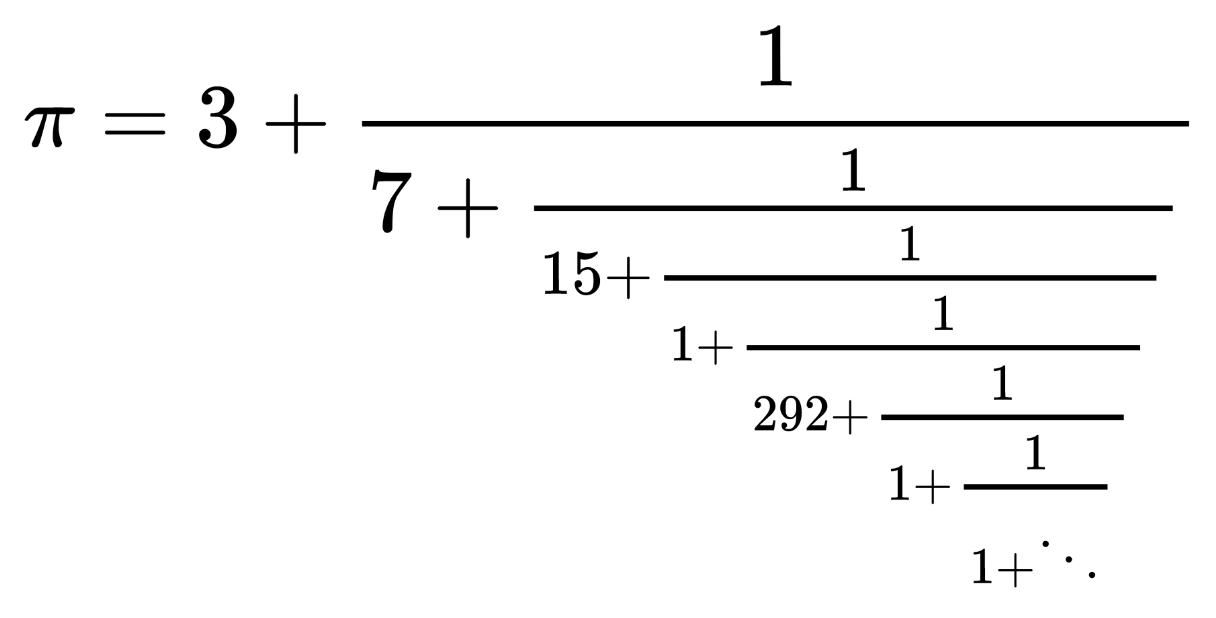
or in short notation [3;7,15,1,292,1,1,1,2,...]. Terminating the continued fraction gives the fractions 3/1, 22/7, 333/106, 355/113, ... So the fraction 355/113 appears as [3;7,15,1].
The approximation is particularly good if the continued fraction is terminated before a large denominator, here 292. If you go far enough, there are arbitrarily large denominators. The next one larger than 292 occurs after 307 steps and is 436. The corresponding p and q have 154 digits, the error to π is in the 311th digit, and the efficiency is only R = 1.007. There is probably no rational approximation more efficient than 355/113, although I know of no proof.
This led him to two hypotheses:
I. The "gravitational constant" is not constant, but decreases inversely proportional to the age of the universe.
II. The total mass in the universe grows proportionally to the square of time.
Pascual Jordan took up these hypotheses and proposed modifications of Einstein's general theory of relativity that fit Dirac's hypotheses. He also postulated that the Earth has expanded over the course of Earth's history due to decreasing gravity.
Anecdote 1: When Wolfgang Pauli heard of Jordan's theory that the mass of the universe increases quadratically with time, he commented on it with regard to Jordan's ever-increasing corpulence with the remark that it was pure anthropomorphism: Jordan was projecting his own development onto space .
Anecdote 2: In the 1950s, the physicist and philosopher Carl Friedrich von Weizsäcker proposed a theory of the universe that is based on so-called quantum theoretical "ur-alternatives". An alternative is a yes-no question. In a lecture he stated that the state of the universe is determined by a finite number of ur-alternatives, and estimated that the number of corresponding yes-no questions is given by the cube of Dirac's large number and is about 10120. Harry Lehmann (my graduate father), who was present and knew Weizsäcker from their time in Göttingen, shouted "minus one". In response to Weizsäcker's astonished question, "What do you mean, Mr. Lehmann?", he replied "10120 minus 1. One question has already been decided: I think your theory is wrong."
Addendum: Dirac's hypotheses are now considered refuted.
The key lies in the Riemann zeta function:
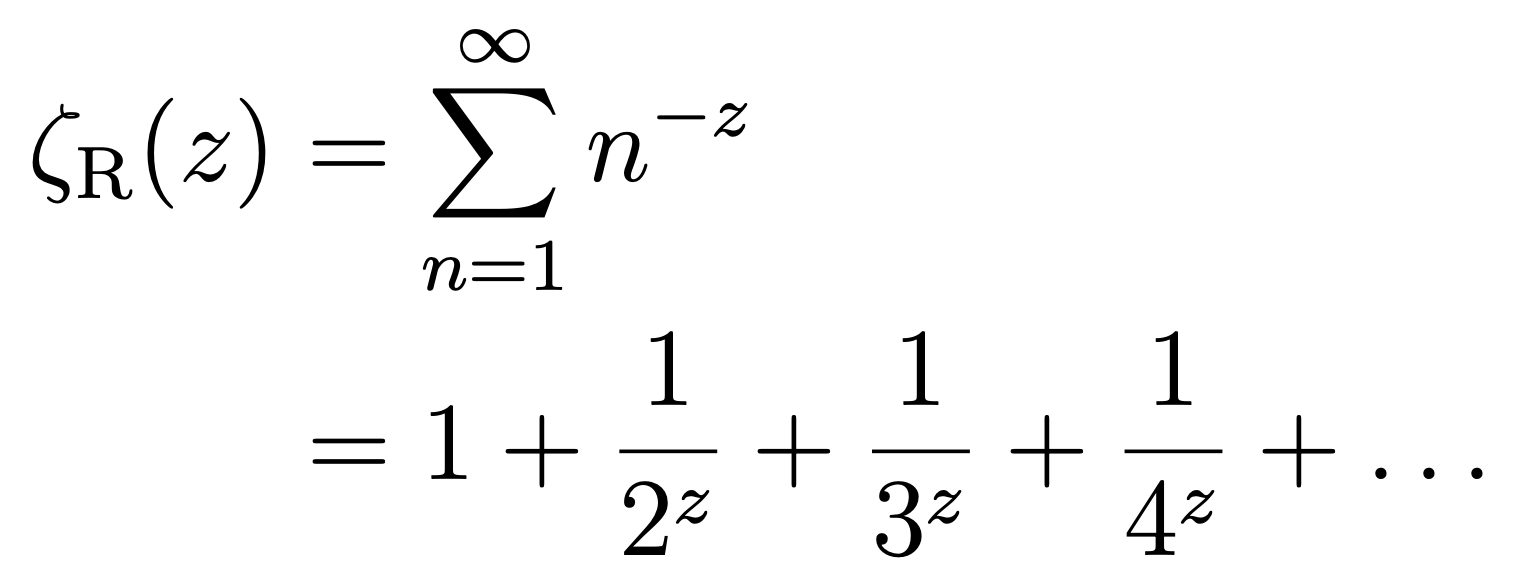
Here the variable z is a complex number. For example, for z=2 you get the sum of the inverse square numbers that Euler calculated:

For z = -1 one would get the desired sum of the natural numbers; however, the series does not converge there. The trick is that the zeta function can be continued analytically to the entire complex plane, except for one pole at z = 1. And at z = -1 you find the value -1/12. This value of the zeta function is what actually occurs in string theory.
By the way, the "sum of squares" (z = -2) is zero.
If you are interested in details, you can find a sketch of the derivation in an article by John Baez.