Fun facts für Zahlenfreunde

6174

Lass eine befreundete Person eine beliebige vierstellige Zahl wählen, nur dürfen nicht alle 4 Ziffern gleich sein. Beispiel 7173. Sie soll nun daraus zwei neue Zahlen bilden, indem die Ziffern absteigend und aufsteigend geordnet werden, und deren Differenz berechnen. Beispiel 7731 - 1377 = 6354. Mit dieser Zahl wird das Verfahren wiederholt. Nach mehreren Schritten (max. 7) erhält man eine Zahl, die sich reproduziert.

Du ziehst aus der Tasche einen Zettel, auf dem das Ergebnis steht: 6174.

Die Eulersche Zahl e und der Zufall

Man erzeuge reelle Zufallszahlen zwischen 0 und 1, gleichverteilt (mittels Computer, oder Zollstock plus Reiskorn). Diese addiert man, bis die Summe größer als 1 ist, und notiert, wieviele Zahlen dafür benötigt wurden. Dann das gleiche von vorn. Wieviele Zufallszahlen benötigt man im Mittel?

Antwort: 2,71828… = e, die Eulersche Zahl

Irrationale Potenzen

Bekanntlich sind irrationale Zahlen diejenigen, die sich nicht als Bruch darstellen lassen. Prominentes Beispiel ist √2. Ein sehr schwieriges Thema der Mathematik ist die Frage, wann Potenzen a^b rational oder irrational sind (siehe Gelfond-Schneider-Theorem).

Frage: Gibt es irrationale Zahlen a und b, für welche die Potenz a^b rational ist?

Erstaunlicherweise gibt es einen elementaren Beweis dafür, dass es das gibt:

Optimaler Hauskauf mit e

Mal wieder ein Fun fact für Zahlenfreunde, und wieder mit Eulers Konstante e.

Angenommen, Sie möchten ein Haus kaufen. Makler M hat die besten Häuser zu bieten. Er bietet Ihnen N Häuser der Reihe nach zur Ansicht an. Leider gilt folgende Regel: Lehnen Sie ein Haus ab, steht es danach nicht mehr zur Verfügung. Wie sollen Sie vorgehen?

Die optimale Strategie geht so: Sie schauen sich den Anteil x (0 < x <1) der Häuser an. Danach wählen Sie das erste Haus aus, das Ihnen besser gefällt, als alle vorherigen.
Die Strategie ist optimal für die Wahl x = 1/e ~ 0.37

Es gibt natürlich keine Garantie, dass Sie das für Sie beste Haus bekommen, mit viel Pech kann es sogar das schlechteste sein, aber für x = 1/e ist die Wahrscheinlichkeit am größten, dass Sie das für Sie beste Haus erwischen.

Die Nachkommastellen von π

Es ist bekannt, dass die Folge der Dezimalstellen der Kreiszahl π = 3,1415926535... nicht abbricht und auch nicht periodisch ist: π ist irrational. Viele Millionen Nachkommastellen sind berechnet worden, und die Ziffernfolge sieht so aus wie eine Folge von zufällig gewürfelten Ziffern (was sie natürlich nicht ist). Diese Eigenschaft von π („π ist normal“) konnte allerdings bis jetzt noch nicht bewiesen werden.

Kurioserweise gab es eine zeitlang Zweifel: William Shanks veröffentlichte 1853 das Ergebnis seiner jahrelangen Berechnung von 607 Nachkommastellen von π, die er später auf 707 Stellen ausdehnte. Augustus De Morgan fiel auf, dass unter den 607 Stellen die Ziffer 7 nur 44 mal vorkommmt. Die Abweichung von der wahrscheinlichsten Anzahl 61 ist deutlich größer als man statistisch erwarten würde, und der Verdacht kam auf, dass die Ziffern nicht gleichverteilt sind.

Erst 1946 stellte D. Ferguson fest, dass Shanks einen Fehler gemacht hatte und nur die ersten 527 Stellen stimmten. Nach heutigem Stand scheint π „normal“ zu sein.

Übrigens, wenn es so ist, würde jede endliche Folge von Ziffern irgendwo darin vorkommen; z.B. kommt die Folge 31415926 zuerst an der 50366472-ten Stelle nach dem Komma vor. Auf der Pi-Search Page kann man seinen Geburtstag oder andere Folgen suchen.

Euler, Gauß und 163

Eine Fun story für Zahlenfreunde.

Zwei bemerkenswerte Sachverhalte:

A. Setzt man in den quadratischen Ausdruck n² - n + 41 nacheinander die Zahlen n = 1, 2, 3, etc. bis n = 40 ein, so erhält man jeweils Primzahlen. Dies hat Leonhard Euler 1772 beobachtet.

B. Die Zahl exp( π √163 ) = 262537412640768743,99999999999925... ist fast genau eine ganze Zahl.

Fun fact: die beiden Sachverhalte hängen zusammen.

1. Die Lösungen der quadratischen Gleichung x² - x + 41 = 0 mit dem Eulerschen Polynom sind die komplexen Zahlen 1/2 ± i/2 √163, mit der Primzahl 163. Fügt man ganzzahlige Koeffizienten k und m hinzu, erhält man den Zahlbereich, der aus den komplexen Zahlen der Form k/2 + i m/2 √163 besteht. Diese lassen sich innerhalb des Bereiches addieren, subtrahieren, multiplizieren und dividieren.

2. In Zahlbereichen ähnlicher Art mit einer Zahl d anstelle von 163 gilt aber nicht immer die Eindeutigkeit der Primfaktorzerlegung. Gauß bewies 1801 in seinem monumentalen Jugendwerk „Disquisitiones arithmeticae“ Resultate, welche gleichbedeutend damit sind, dass die Primfaktorzerlegung eindeutig ist für die 9 Primzahlen: 1, 2, 3, 7, 11, 19, 43, 67 und 163. Diese werden Heegner-Zahlen genannt (s.u.), obwohl sie eigentlich nach Gauß benannt werden sollten. Es kann gezeigt werden, dass aus diesem Resultat der Sachverhalt A folgt.

3. In der Funktionentheorie gibt es eine prominente Funktion, Felix Kleins „modulare Invariante“ j(t). In seinem „Lehrbuch der Algebra“ demonstriert Heinrich Weber 1895, das j(t) eine ganze Zahl ist, wenn t = 1/2 + i/2 √d und d eine der obigen Heegner-Zahlen ist. j(t) besitzt eine Reihenentwicklung mit dem führenden Term exp(-2 π i t). Daraus folgt schließlich, dass exp( π √163 ) fast genau eine ganze Zahl ist.

4. Gibt es jenseits von 163 weitere Heegner-Zahlen? Eine Reihe prominenter Mathematiker hatte sich bereits mit diesem Problem befasst, als der pensionierte Ingenieur und Mathematiker Kurt Heegner 1952 einen raffinierten Beweis dafür publizierte, dass 163 die größte sei. Der Beweis enthielt jedoch Lücken. Andere, vollständige Beweise wurden 1966 von Harold Stark und Alan Baker erbracht. Die Lücken in Heegners Beweis wurden 1969 von Stark geschlossen.

Die effizienteste rationale Approximation für π

Es ist bekannt, dass die Kreiszahl π = 3,141592653589... irrational ist, sich also nicht als Bruch darstellen lässt. Aber sie lässt sich beliebig genau durch Brüche p/q approximieren.

Populär ist 22/7 = 3,1428... Bemerkenswert ist der Bruch 355/113 = 3,14159292..., der vom chinesischen Mathematiker Zu Chongzhi im 5. Jahrhundert entdeckt wurde und sich leicht merken lässt (113355). Diese Approximation ist sehr effizient, da sie 7 Stellen von π (incl. der 3) durch 6 Ziffern wiedergibt. Gibt es noch effizientere rationale Approximationen?

Betrachten wir als Maß für die Effizienz die Anzahl korrekter Stellen geteilt durch die Anzahl benötigter Ziffern. Etwas besser mathematisch formuliert ist es das Verhältnis R = - log(|π - p/q|) / log(pq).
Für 22/7 ist R = 1,325 und für 355/113 ist R = 1,428. Geht es noch effizienter?

Die besten rationalen Approximationen für irrationale Zahlen werden durch reguläre Kettenbrüche geliefert. Für π lautet er

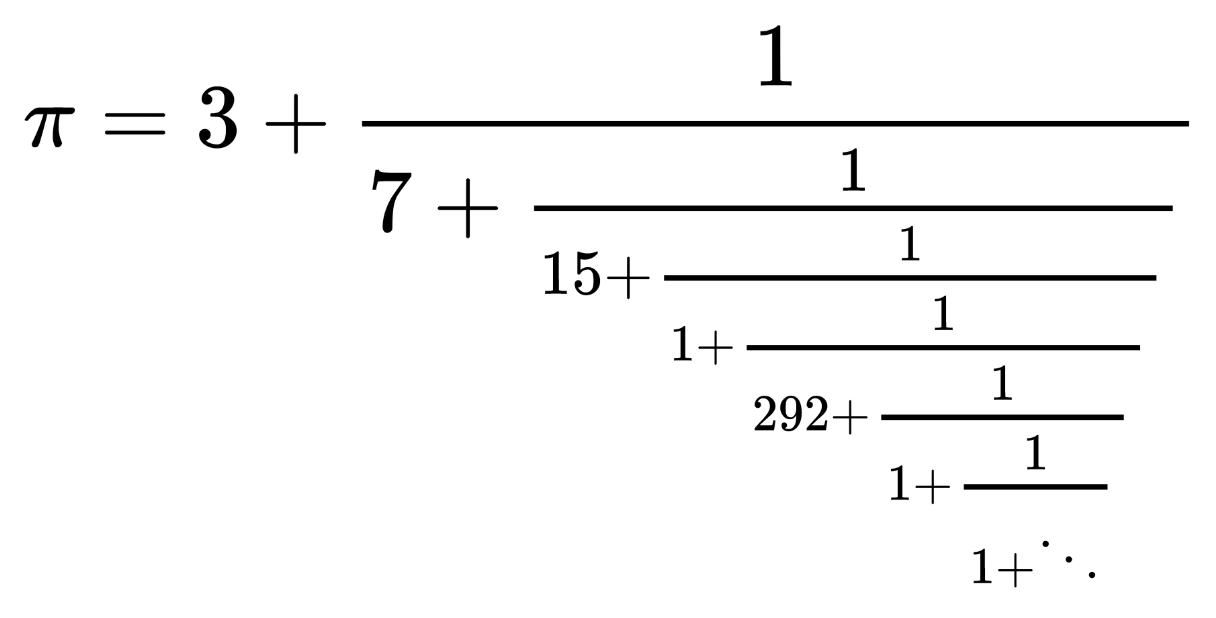
bzw. in Kurznotation [3;7,15,1,292,1,1,1,2,...]. Abbrechen des Kettenbruchs gibt die Brüche 3/1, 22/7, 333/106, 355/113, ... Da taucht der Bruch 355/113 also auf als [3;7,15,1].

Besonders gut ist die Approximation, wenn der Kettenbruch vor einem großen Nenner abgebrochen wird, hier die 292. Geht man weit genug, gibt es beliebig große Nenner. Der nächste, der größer als 292 ist, tritt nach 307 Schritten auf und lautet 436. Die entsprechenden p und q haben 154 Stellen, der Fehler zu π ist in der 311ten Stelle und die Effizienz ist nur R = 1,007. Wahrscheinlich gibt es keine effizientere rationale Approximation als 355/113, allerdings kenne ich keinen Beweis.

Die Summe aller natürlichen Zahlen

Man muss nicht gut in Mathe sein, um zu wissen, dass die Summe 1 + 2 + 3 + ... keine endliche Zahl sein kann, d. h. unendlich ist. Erstaunlicherweise findet man bei dem genialen Mathematiker S. Ramanujan die Gleichung 1 + 2 + 3 + ... = - 1/12. Auch L. Euler kannte sie wahrscheinlich. Sogar in der Stringtheorie taucht sie auf. Was steckt dahinter? Auf YouTube kann man Videos finden, in denen diese seltsame Gleichung „hergeleitet“ wird. Warnung! Diese Herleitungen sind mathematisch nicht gültig. Was bedeutet die Gleichung dann aber?

Der Schlüssel liegt in der Riemannschen Zeta-Funktion:

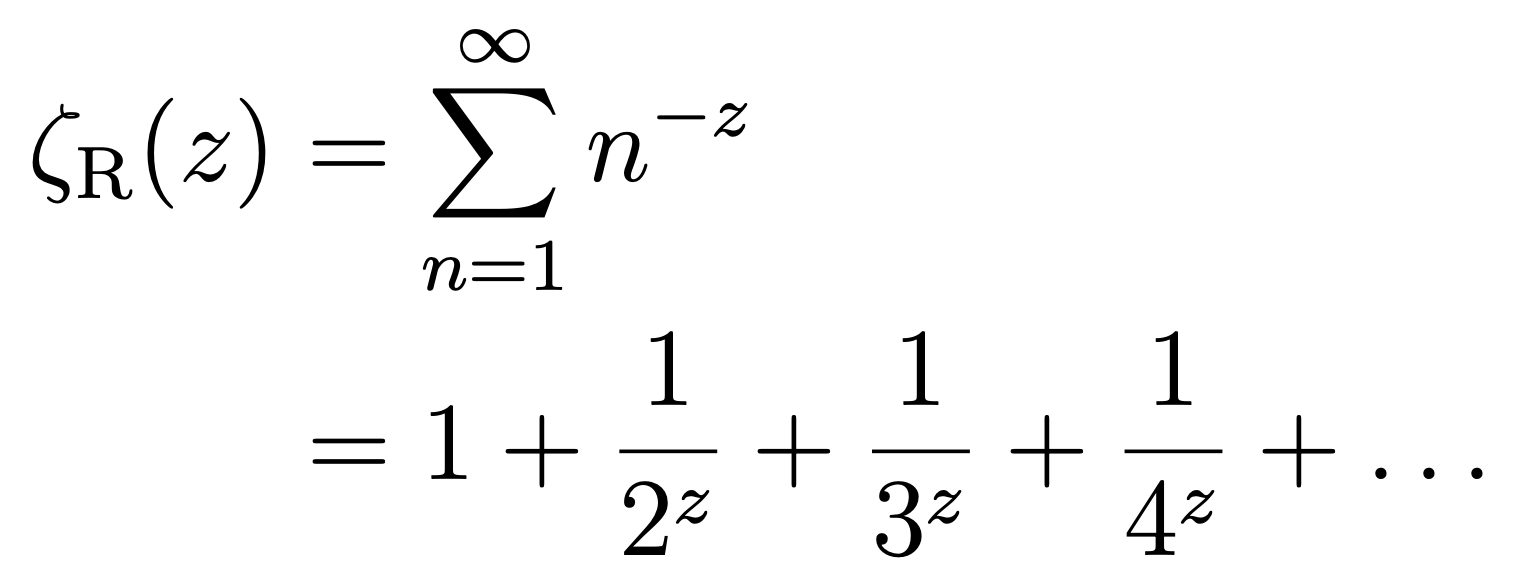
Die Variable z ist hier eine komplexe Zahl. Für z = 2 erhält man z. B. die Summe der inversen Quadratzahlen, die Euler berechnet hat:

Für z = -1 würde man die gesuchte Summe der natürlichen Zahlen erhalten; allerdings konvergiert die Reihe dort nicht. Der Witz ist nun, dass sich die Zeta-Funktion in die gesamte komplexe Zahlenebene eindeutig analytisch fortsetzen lässt, bis auf einen Pol bei z = 1. Und bei z = -1 findet man den Wert -1/12. Dieser Wert der Zeta-Funktion ist das, was tatsächlich in der Stringtheorie vorkommt.
Übrigens ist die „Summe der Quadratzahlen“ (z = -2) gleich Null.

Wer an Details interessiert ist, kann eine Skizze der Herleitung z. B. in einem Artikel von John Baez nachlesen.

Die Zahl Deines Lebens: die Champernowne-Zahl

Unter den reellen Zahlen gibt es speziell die transzendenten Zahlen. Diese sind nicht Lösung einer algebraischen Gleichung, d.h. sie sind nicht Nullstelle eines Polynoms mit ganzzahligen Koeffizienten. Die Wurzel aus 2 ist zwar irrational, aber nicht transzendent, denn sie ist Lösung von x² - 2 = 0. Liouville hat 1844 als Erster die Existenz transzendenter Zahlen bewiesen und explizite Beispiele konstruiert. Die wohl bekanntesten transzendenten Zahlen sind π und die Eulersche Zahl e. Die Beweise ihrer Transzendenz sind recht kompliziert.

Eine besondere transzendente Zahl ist die Champernowne-Zahl Q = 0,123456789101112131415... Man erkennt das offensichtliche Bildungsgesetz der Nachkommastellen. Q ist sogar „normal“ bzw. ein „Zahlenuniversum“. Das heißt, dass jede endliche Folge von natürlichen Zahlen irgendwo in den Nachkommastellen von Q vorkommt. David Champernowne lieferte 1933 mit Q die erste explizit konstruierte normale Zahl.

Ihre Kreditkarten-Pin, ihre IBAN, ihre Steuernummer kommen irgendwo in den Ziffern von Q vor. Nun stellen Sie sich vor, es gäbe ein Video mit Ihrer kompletten Lebensgeschichte, inklusive der noch kommenden Ereignisse. Auf einer sehr großen Festplatte gespeichert wird es durch eine sehr sehr lange Folge von Nullen und Einsen dargestellt. In dieser Form kommt das Video irgendwo in den fernen Tiefen der Ziffern von Q vor. Q enthält also die Information über Ihr gesamtes Leben. Leider hilft Ihnen das aber nicht, denn Q enthält in gleicher Weise auch alle möglichen falschen Lebensgeschichten.

Dirac, die großen Zahlen, und zwei Anekdoten

Der Physiker Paul Dirac, Pionier der Quantentheorie, Entdecker der Dirac-Gleichung und Nobelpreisträger, wies 1937 auf folgende bemerkenswerte Sachverhalte hin:
Das Alter des Universums, geteilt durch eine typische atomare Zeitskala beträgt ungefähr 10⁴⁰ (eine 1 mit 40 Nullen). Der genaue Wert spielt hier keine Rolle; es geht um die Größenordnung.
Die Gravitationskraft zwischen Proton und Elektron, geteilt durch deren elektrische Anziehungskraft, beträgt ungefähr 10^-40.
Die im Universum enthaltene Masse, geteilt durch die Protonenmasse, beträgt ungefähr 10⁸⁰.

Dies führte ihn zu zwei Hypothesen:
I. Die „Gravitationskonstante“ ist nicht konstant, sondern nimmt umgekehrt proportional zum Alter des Universums ab.
II. Die Gesamtmasse im Universum wächst proportional zum Quadrat der Zeit.

Pascual Jordan hat diese Hypothesen aufgegriffen und Modifikationen der Einsteinschen Allgemeinen Relativitätstheorie vorgeschlagen, die zu den Diracschen Hypothesen passen. Außerdem hat er postuliert, dass die Erde sich aufgrund der abnehmenden Gravitation im Laufe der Erdgeschichte ausgedehnt hat.

Anekdote 1: Als Wolfgang Pauli von Jordans Theorie hörte, dass die Masse des Universums im Laufe der Zeit quadratisch zunimmt, kommentierte er es im Hinblick auf Jordans stetig zunehmende Leibesfülle mit der Bemerkung, dass sei reiner Anthropomorphimus, Jordan projiziere seine eigene Entwicklung auf das Weltall.

Anekdote 2: Der Physiker und Philosoph Carl Friedrich von Weizsäcker schlug in den 1950er Jahren eine Theorie des Universums vor, die auf sogenannten quantentheoretischen Ur-Alternativen beruht. Eine Alternative ist eine Ja-Nein-Frage. In einem Vortrag trug er vor, dass der Zustand des Universums durch eine endliche Zahl von Ur-Alternativen festgelegt ist, und schätzte ab, dass die Anzahl der entsprechenden Ja-Nein-Fragen durch die dritte Potenz der Diracschen großen Zahl gegeben ist und etwa 10¹²⁰ beträgt. Der anwesende Harry Lehmann (mein Diplom-Vater), mit Weizsäcker aus Göttinger Zeiten bekannt, rief „minus Eins“. Auf Weizsäckers verwunderte Frage „Wie meinen Sie das, Herr Kollege Lehmann?“ antwortete dieser „10¹²⁰ minus 1. Eine Frage ist nämlich schon entschieden: ich halte Ihre Theorie für falsch.“

Nachtrag: die Diracschen Hypothesen gelten heute als widerlegt.

137, Eddington und Pauli

Die Stärke der elektromagnetischen Wechselwirkungen wird durch eine Zahl α, die „Sommerfeldsche Feinstrukturkonstante“, charakterisiert. Ihr Wert beträgt ungefähr 1/137. Auf 4 Nachkommastellen genau ist ihr Inverses 137,036. Diese Zahl ist von fundamentaler Bedeutung für die Physik. Richard Feynman schreibt: „Sie ist seit ihrer Entdeckung vor über 50 Jahren ein Mysterium. Sie werden sogleich wissen wollen, woher diese Zahl stammt. Niemand weiss es. Sie ist eine der grössten verdammten Geheimnisse der Physik: eine magische Zahl, die zu uns gekommen ist, ohne dass irgendjemand sie versteht.“

Vor fast 80 Jahren war der empirische Wert noch mit der exakten Zahl 137 verträglich. Viele Physiker, darunter auch Dirac und Heisenberg, haben darüber gerätselt, ob ein besonderer Grund hinter dieser Zahl steckt. Arthur S. Eddington, der weithin durch die Messung der Lichtablenkung nahe der Sonne 1919 bekannt ist, veröffentlichte 1918 eine obskure Herleitung, nach welcher der genaue Wert 136 betragen müsste. Später kam er zu einer modifizierten Theorie mit dem exakten Wert 137, in der er auch eine Formel für die exakte Zahl der Protonen im Universum angab. Diese numerologischen Versuche sind aber nicht ernst zu nehmen.

Auch Wolfgang Pauli vermutete einen tieferen Grund für den Wert 137. Er diskutierte sogar mit dem Psychoanalytiker C.G. Jung über die mögliche besondere Bedeutung der Zahl 137 und brachte sie mit der Kabbala in Verbindung. Vor seinem Tod im Jahr 1958 kam er in einem Hospital in Zürich ausgerechnet auf das Zimmer 137, was ihn sehr beunruhigte.

Es gibt zahlreiche Versuche, den Wert der Feinstrukturkonstanten durch einfache Formeln darzustellen. Z. B. veröffentlichte A. Wyler 1969 dafür folgenden Ausdruck.

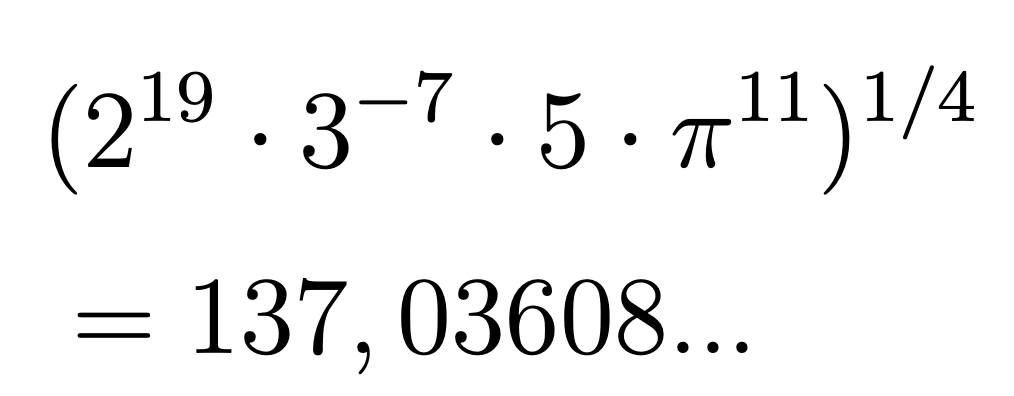
Es stellt sich allerdings heraus, dass man viele solche Formeln finden kann, ohne dass etwas dahinter steckt.

Heute weiß man, dass die „Feinstrukturkonstante“ von der Energie der betrachteten Prozesse abhängt und bei hohen Energien größer wird. Somit hat sich die Bedeutung des Zahlenwertes 137 relativiert.

Zum Schluss eine Geschichte. Als Pauli in den Himmel kam, verlangte er, Gott zu sprechen und fragte ihn nach dem Wert der Feinstrukturkonstanten. Gott holte einen Stapel Notizen hervor und begann an der Tafel vorzurechnen. Nach drei Minuten rief Pauli „Das ist doch falsch!“

Die sehr runden Zahlen

Betrachten wir die Zahl 20. Unter den Zahlen, die kleiner als 20 sind (außer der 1), sind einige, die mit 20 = 2 x 2 x 5 einen oder mehrere gemeinsame Teiler haben, z.B. alle geraden und 5 und 15. Die übrigen, also 3, 7, 9, 11, 13, 17 und 19, sind teilerfremd zu 20. Bis auf die 9 sind es Primzahlen.

Machen wir die gleiche Untersuchung mit der Zahl 18, finden wir, dass 5, 7, 11, 13 und 17 teilerfremd zu 18 sind. Diesmal sind es nur Primzahlen.

Frage: für welche Zahlen N gilt, dass alle Zahlen kleiner als N, die teilerfremd zu N sind, auch Primzahlen sind?

Durch Probieren findet man 3, 4, 6, 8, 12, 18, 24 und 30. Sie werden auch "sehr runde Zahlen" genannt. Gibt es noch weitere?

Tatsächlich ist 30 die größte „sehr runde“ Zahl. Ein Beweis dafür wurde 1907 von dem Münsteraner Studenten Bonse gefunden. Relativ einfach ist einzusehen, dass es genügt, für n>3 die Ungleichung (p_n+1)² < p₁ p₂ ... p_n zu zeigen, wobei p_n die Folge der Primzahlen ist. Der Beweis dieser Ungleichung mit elementaren Mitteln, d.h. ohne die schweren Geschütze der analytischen Zahlentheorie, ist aber schwierig.

Literatur:
H. Rademacher and O. Toeplitz, Von Zahlen und Figuren, Springer Verlag, Berlin, 1930, Kapitel 22.
R. Honsberger, Mathematical Gems, The Two-Year College Mathematics Journal 10 (1979) 195-197.
The On-Line Encyclopedia of Integer Sequences, Sequence A048597.

Das Menage-Problem von Edouard Lucas

Viele kombinatorische Probleme haben Lösungen, die man als einigermaßen einfache Formel niederschreiben kann. Z.B. die Anzahl verschiedener Tanzpaare, die man in einem Tanzkursus bilden kann, oder die Anzahl verschiedener Klammerungen eines Produktes. Umso erstaunlicher, wie kompliziert die Lösung des folgenden Problems ist:

Auf wieviele Weisen M_n kann man n Ehepaare an einen runden Tisch setzen, wenn jede Frau zwischen zwei Männern, aber keine Frau neben ihrem eigenen Mann sitzen soll?

Die Aufgabe stammt von dem Mathematiker E. Lucas (1842-1891). Durch Probieren findet man M₂ = 0, M₃ = 12 und M₄ = 96. Gibt es eine allgemeine Formel für M_n?

Die Aufgabe wurde von Mathematikern gelöst. Es stellt sich heraus, dass die Lösung recht kompliziert ist. Die Anzahl der Möglichkeiten, wie sich die Frauen platzieren können, findet man leicht. Sie beträgt 2 n! („2 mal n Fakultät“). Aber die Anzahl A_n der Möglichkeiten, sodann die Männer zu platzieren, widersetzt sich einer elementaren Lösung.

Laisant fand 1891 nach langwierigen Überlegungen eine Rekursionsformel:
(n - 1) A_n+1 = (n² -1) A_n + (n + 1) A_n-1 + 4 (-1)ⁿ.
Immerhin lassen sich damit die Werte von A_n berechnen, z.B. A₃ = 1, A₄ = 2, A₅ = 13, A₆ = 80 u.s.w., und daraus M_n = 2 n! A_n, nämlich M₃ = 12, M₄ = 96, M₅ = 3120, M₆ = 115200, etc.
Gibt es dafür eine geschlossene Formel? Ja, sie lautet

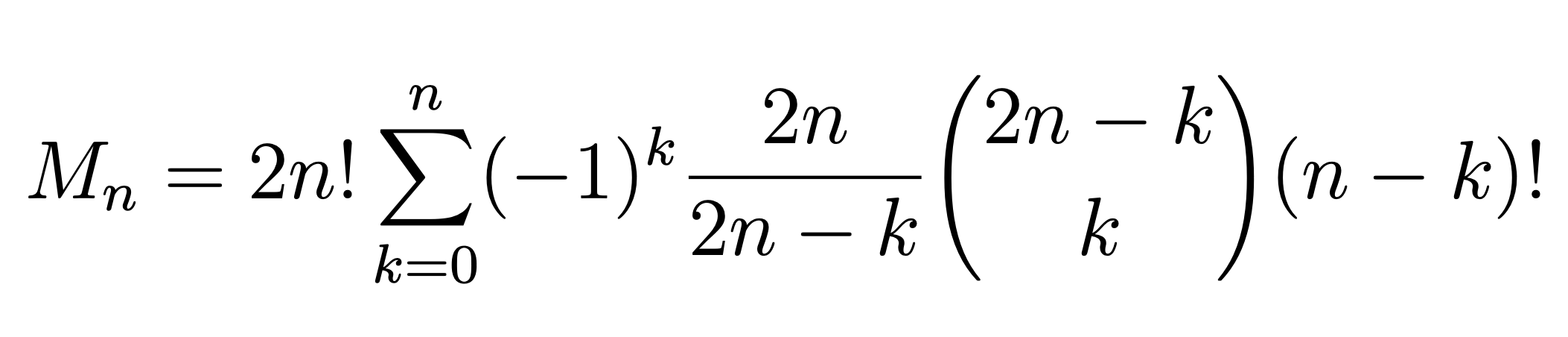
aber leider handelt es sich um eine komplizierte Summe, die die Berechnung nicht erleichtert.

Hinweise nehme ich gerne entgegen.
G. Münster