



Next: Inverse quantum statistics
Up: The Bayesian approach
Previous: Basic notations
Contents
Before applying the Bayesian framework to quantum theory,
we shortly present one of its standard applications:
the case of (Gaussian) regression.
(For more details see for example [34].)
This also provides an example for
the relation between the Bayesian maximum posterior approximation
and the minimization of regularized error functionals.
A regression model is a model with Gaussian likelihoods,
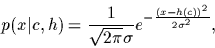 |
(6) |
with fixed variance 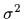 .
The function
.
The function 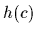 is known as regression function.
(In regression, one often writes
is known as regression function.
(In regression, one often writes
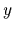 for the dependent variable, which is
for the dependent variable, which is 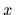 in our notation,
and
in our notation,
and 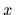 for the ``condition''
for the ``condition'' 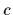 .)
Our aim is to determine an approximation for
.)
Our aim is to determine an approximation for 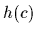 using observational data
using observational data 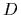 =
=
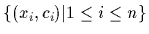 .
Within a parametric approach
one searches for an optimal approximation
in a space of parameterized regression functions
.
Within a parametric approach
one searches for an optimal approximation
in a space of parameterized regression functions
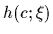 .
For example, in the simple cases of a constant or a linear regression
such a parameterization would
be
.
For example, in the simple cases of a constant or a linear regression
such a parameterization would
be 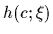 =
= 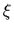 or
or
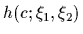 =
=
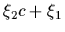 , respectively.
If the parameterization is restrictive enough
then a prior term
, respectively.
If the parameterization is restrictive enough
then a prior term 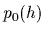 is not needed
and maximizing the likelihood over all data
is not needed
and maximizing the likelihood over all data 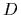 is thus equivalent to minimizing
the squared error,
is thus equivalent to minimizing
the squared error,
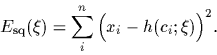 |
(7) |
There are, however,
also very flexible parametric approaches, which usually do require
additional a priori information.
An example of such a nonlinear one-parameter family
has been given by Vapnik
and is shown in Fig. 1.
Without additional a priori information,
which may for example restrict the number of oscillations,
such functions
can in most cases not be expected to lead to useful predictions.
Nonparametric approaches, which treat the
numbers 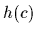 as single degrees of freedom,
are even more flexible and do always require a prior
as single degrees of freedom,
are even more flexible and do always require a prior 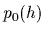 .
For nonparametric approaches such a prior
can be formulated in terms of the function values
.
For nonparametric approaches such a prior
can be formulated in terms of the function values 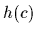 .
A technically very convenient choice is a Gaussian process prior
[48,49],
.
A technically very convenient choice is a Gaussian process prior
[48,49],
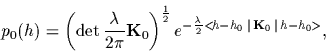 |
(8) |
with mean 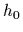 , representing a
reference or template for the regression function
, representing a
reference or template for the regression function 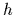 ,
and inverse covariance
,
and inverse covariance
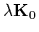 given by a
real symmetric, positive (semi-)definite
operator
scaled by
given by a
real symmetric, positive (semi-)definite
operator
scaled by 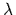 and acting on functions
and acting on functions 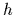 .
The operator
.
The operator 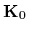 defines the scalar product,
defines the scalar product,
![\begin{displaymath}
<\!h-h_0\,\vert\,{\bf K}_0\,\vert\,h-h_0\!>
=
\int \!dc \, d...
...c)]
\, {\bf K}_0(c,c^\prime) \,
[h(c^\prime )-h_0(c^\prime)]
.
\end{displaymath}](img108.gif) |
(9) |
Typical priors enforce the regression function 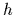 to be smooth.
Such smoothness priors are implemented by choosing differential operators
for
to be smooth.
Such smoothness priors are implemented by choosing differential operators
for 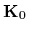 .
For example, taking for
.
For example, taking for 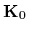 the negative Laplacian
and choosing a zero mean
the negative Laplacian
and choosing a zero mean 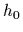 =
= 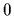 ,
yields
,
yields
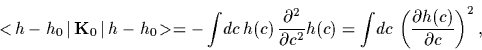 |
(10) |
where we integrated by parts
assuming vanishing boundary terms.
In statistics one often prefers inverse covariance operators
with higher derivatives to obtain smoother regression functions
[16, 50-55]. An example of such a prior with higher derivatives
is a ``Radial Basis Functions'' prior
with the pseudo-differential operator
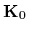 =
=
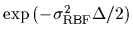 as inverse covariance.
as inverse covariance.
Maximizing the posterior 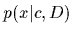 for a Gaussian prior (8)
is equivalent
to minimizing the regularized error functional
for a Gaussian prior (8)
is equivalent
to minimizing the regularized error functional
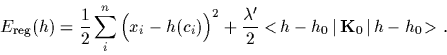 |
(11) |
The ``regularization'' parameter
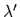 =
=
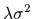 ,
representing a so called hyperparameter,
controls the balance between empirical data
and a priori information.
In a Bayesian framework
one can include a hyperprior
,
representing a so called hyperparameter,
controls the balance between empirical data
and a priori information.
In a Bayesian framework
one can include a hyperprior 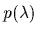 and either integrate over
and either integrate over 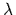 or determine an optimal
or determine an optimal 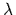 in maximum posterior approximation
[22,26].
Alternative ways to determine
in maximum posterior approximation
[22,26].
Alternative ways to determine 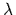 are
crossvalidation techniques[16],
the discrepancy and
the self-consistent method [56].
For example in the case of a smoothness prior,
a larger
are
crossvalidation techniques[16],
the discrepancy and
the self-consistent method [56].
For example in the case of a smoothness prior,
a larger
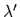 will result in a smoother regression function
will result in a smoother regression function 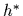 .
It is typical for the case of regression
that the regularized error functional
.
It is typical for the case of regression
that the regularized error functional
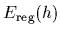 is quadratic in
is quadratic in 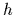 .
It is therefore easily minimized
by setting the functional derivative with respect to
.
It is therefore easily minimized
by setting the functional derivative with respect to 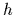 to zero, i.e.,
to zero, i.e.,
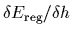 =
=
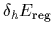 = 0.
This stationarity equation is then linear in
= 0.
This stationarity equation is then linear in 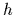 and thus has a unique solution
and thus has a unique solution 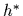 .
(This is equivalent to so called kernel methods
with kernel
.
(This is equivalent to so called kernel methods
with kernel
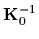 .
It is specific for regression with Gaussian prior
that, given
.
It is specific for regression with Gaussian prior
that, given
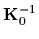 , only an
, only an
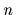 -dimensional equation has to be solved to obtain
-dimensional equation has to be solved to obtain 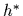 .
)
As the resulting maximum posterior solution
.
)
As the resulting maximum posterior solution
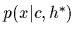 is Gaussian by definition,
we find for its mean
is Gaussian by definition,
we find for its mean
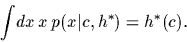 |
(12) |
It is not difficult to check that,
for regression with a Gaussian prior,
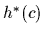 is also equal to the mean
is also equal to the mean
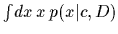 of the exact predictive density
(3).
Furthermore it can be shown that,
in order to minimize the squared error
of the exact predictive density
(3).
Furthermore it can be shown that,
in order to minimize the squared error ![$[x-h(c)]^2$](img127.gif) for (future) test data,
it is optimal to predict outcome
for (future) test data,
it is optimal to predict outcome 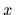 =
= 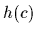 for situation
for situation 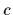 .
.
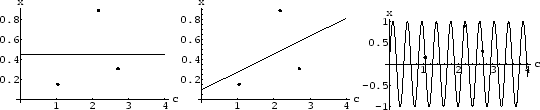
Figure 1:
Examples of parametric regression
functions with increasing flexibility (with 3 data points).
L.h.s: A fitted constant 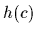 =
=  .
Middle: A linear
.
Middle: A linear 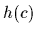 =
=
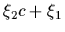 .
R.h.s: The function
.
R.h.s: The function 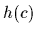 =
= 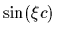 can fit an arbitrary number of data points
(with different
can fit an arbitrary number of data points
(with different 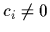 and
and 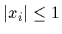 )
well [17].
Additional a priori information becomes especially important
for flexible approaches.
)
well [17].
Additional a priori information becomes especially important
for flexible approaches.
 |
In the following sections we will apply the Bayesian formalism
to quantum theory.
Hence, training data 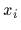 will represent the results of
measurements on quantum systems
and conditions
will represent the results of
measurements on quantum systems
and conditions 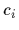 will describe the kind of measurements performed.
Being interested in the determination of quantum potentials
our hypotheses
will describe the kind of measurements performed.
Being interested in the determination of quantum potentials
our hypotheses 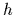 will in the following represent potentials
will in the following represent potentials 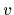 .
.




Next: Inverse quantum statistics
Up: The Bayesian approach
Previous: Basic notations
Contents
Joerg_Lemm
2000-06-06
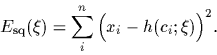
![]() for a Gaussian prior (8)
is equivalent
to minimizing the regularized error functional
for a Gaussian prior (8)
is equivalent
to minimizing the regularized error functional
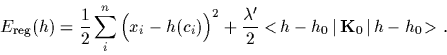

![]() will represent the results of
measurements on quantum systems
and conditions
will represent the results of
measurements on quantum systems
and conditions ![]() will describe the kind of measurements performed.
Being interested in the determination of quantum potentials
our hypotheses
will describe the kind of measurements performed.
Being interested in the determination of quantum potentials
our hypotheses ![]() will in the following represent potentials
will in the following represent potentials ![]() .
.