Next: The Hessians ,
Up: Gaussian prior factor for
Previous: Lagrange multipliers: Error functional
Contents
Again, normalization can also be ensured by parameterization of 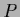 and solving for unnormalized probabilities
and solving for unnormalized probabilities 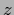 , i.e.,
, i.e.,
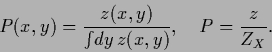 |
(174) |
The corresponding functional reads
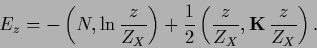 |
(175) |
We have
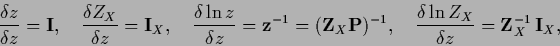 |
(176) |
with diagonal matrix 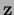 built analogous to
built analogous to 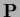 and
and 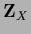 ,
and
,
and
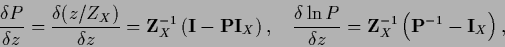 |
(177) |
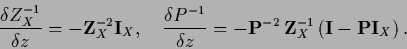 |
(178) |
The diagonal matrices
![$[{\bf Z}_X , {\bf P} ] = 0$](img684.png) commute,
as well as
commute,
as well as
![$[{\bf Z}_X , {\bf I}_X] = 0$](img685.png) ,
but
,
but
![$[ {\bf P} , {\bf I}_X] \ne 0$](img686.png) .
Setting the gradient to zero and using
.
Setting the gradient to zero and using
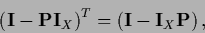 |
(179) |
we find
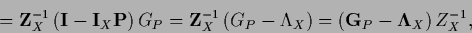 |
(180) |
with 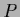 -gradient
-gradient
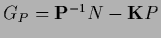 =
=
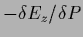 of
of 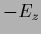 and
and 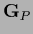 the corresponding diagonal matrix.
Multiplied by
the corresponding diagonal matrix.
Multiplied by 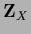 this gives the stationarity equation (172).
this gives the stationarity equation (172).




Next: The Hessians ,
Up: Gaussian prior factor for
Previous: Lagrange multipliers: Error functional
Contents
Joerg_Lemm
2001-01-21
![]() and solving for unnormalized probabilities
and solving for unnormalized probabilities ![]() , i.e.,
, i.e.,