



Next: General Gaussian prior factors
Up: Gaussian prior factor for
Previous: Normalization by parameterization: Error
Contents
The Hessians 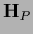 ,
, 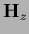
We now calculate the Hessian of the functional 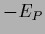 .
For fixed
.
For fixed 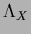 one finds the Hessian
by differentiating again the gradient (166)
of
one finds the Hessian
by differentiating again the gradient (166)
of 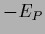
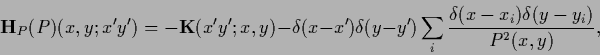 |
(181) |
i.e.,
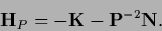 |
(182) |
Here the diagonal matrix
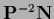 is non-zero only at data points.
is non-zero only at data points.
Including the dependence of 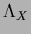 on
on 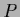 one obtains for the Hessian of
one obtains for the Hessian of 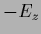 in (175)
by calculating the derivative of the gradient in (180)
in (175)
by calculating the derivative of the gradient in (180)
![\begin{displaymath}
+ 2\, \delta (x-x^\prime)
\int\! dy^{\prime\prime} dx^{\pr...
...e},y^{\prime\prime\prime})
\Big] \frac{1}{ Z_X (x^\prime) },
\end{displaymath}](img705.png) |
(183) |
i.e.,
Here we used
![$[{\bf\Lambda}_X,{\bf I}_X]$](img712.png) = 0.
It follows from the normalization
= 0.
It follows from the normalization
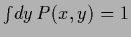 that any
that any 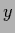 -independent function
is right eigenvector of
-independent function
is right eigenvector of
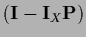 with zero eigenvalue.
Because
with zero eigenvalue.
Because 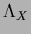 =
=
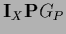 this factor or its transpose is
also contained in the second line of
Eq. (184),
which means that
this factor or its transpose is
also contained in the second line of
Eq. (184),
which means that 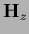 has a zero mode.
Indeed, functional
has a zero mode.
Indeed, functional 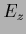 is invariant under multiplication
of
is invariant under multiplication
of 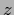 with a
with a 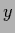 -independent factor. The zero modes can be projected out
or removed by including additional conditions, e.g. by
fixing one value of
-independent factor. The zero modes can be projected out
or removed by including additional conditions, e.g. by
fixing one value of 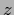 for every
for every 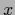 .
.




Next: General Gaussian prior factors
Up: Gaussian prior factor for
Previous: Normalization by parameterization: Error
Contents
Joerg_Lemm
2001-01-21
![]() .
For fixed
.
For fixed ![]() one finds the Hessian
by differentiating again the gradient (166)
of
one finds the Hessian
by differentiating again the gradient (166)
of ![]()
![]() on
on ![]() one obtains for the Hessian of
one obtains for the Hessian of ![]() in (175)
by calculating the derivative of the gradient in (180)
in (175)
by calculating the derivative of the gradient in (180)
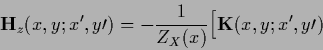
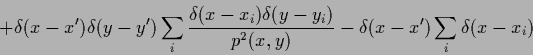
![\begin{displaymath}
+ 2\, \delta (x-x^\prime)
\int\! dy^{\prime\prime} dx^{\pr...
...e},y^{\prime\prime\prime})
\Big] \frac{1}{ Z_X (x^\prime) },
\end{displaymath}](img705.png)