



Next: Quadratic density estimation and
Up: Gaussian prior factors
Previous: Example: Approximate periodicity
Contents
Non-zero means
A prior energy term
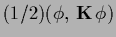 measures the squared
measures the squared 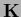 -distance
of
-distance
of 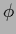 to the zero function
to the zero function  .
Choosing a zero mean function for the prior process
is calculationally convenient for Gaussian priors,
but by no means mandatory.
In particular,
a function
.
Choosing a zero mean function for the prior process
is calculationally convenient for Gaussian priors,
but by no means mandatory.
In particular,
a function 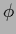 is
in practice often measured relative to some non-trivial base line.
Without further a priori information
that base line can in principle be an arbitrary function.
Choosing a zero mean function that base line does not enter
the formulae
and remains hidden in the realization of the measurement process.
On the the other hand,
including explicitly a non-zero mean function
is
in practice often measured relative to some non-trivial base line.
Without further a priori information
that base line can in principle be an arbitrary function.
Choosing a zero mean function that base line does not enter
the formulae
and remains hidden in the realization of the measurement process.
On the the other hand,
including explicitly a non-zero mean function 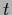 , playing the role of
a function
, playing the role of
a function
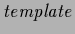 (or reference, target, prototype, base line)
and being technically relatively straightforward,
can be a very powerful tool.
It allows, for example, to
parameterize
(or reference, target, prototype, base line)
and being technically relatively straightforward,
can be a very powerful tool.
It allows, for example, to
parameterize 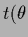 ) by introducing hyperparameters
(see Section 5)
and to specify explicitly different maxima of multimodal functional priors
(see Section 6.
[132,133,134,135,136]).
All this cannot be done by referring to a single baseline.
) by introducing hyperparameters
(see Section 5)
and to specify explicitly different maxima of multimodal functional priors
(see Section 6.
[132,133,134,135,136]).
All this cannot be done by referring to a single baseline.
Hence, in this section we consider error terms of the form
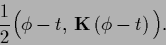 |
(225) |
Mean or template functions 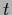 allow an easy and straightforward implementation
of prior information in form of examples for
allow an easy and straightforward implementation
of prior information in form of examples for 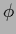 .
They are the continuous analogue of standard training data.
The fact that template functions
.
They are the continuous analogue of standard training data.
The fact that template functions 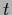 are most times chosen equal to zero, and thus do not appear explicitly
in the error functional,
should not obscure the fact that they are of key importance
for any generalization.
There are many situations where
it can be very valuable to include non-zero prior means explicitly.
Template functions for
are most times chosen equal to zero, and thus do not appear explicitly
in the error functional,
should not obscure the fact that they are of key importance
for any generalization.
There are many situations where
it can be very valuable to include non-zero prior means explicitly.
Template functions for 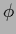 can for example result
from learning done in the past for the same or for similar tasks.
In particular,
consider for example
can for example result
from learning done in the past for the same or for similar tasks.
In particular,
consider for example
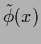 to be the output
of an empirical learning system
(neural net, decision tree, nearest neighbor methods,
to be the output
of an empirical learning system
(neural net, decision tree, nearest neighbor methods,  )
being the result of learning
the same or a similar task.
Such a
)
being the result of learning
the same or a similar task.
Such a
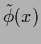 would be a natural candidate
for a template function
would be a natural candidate
for a template function 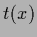 .
Thus, we see that template functions
could be used for example
to allow transfer of knowledge between similar tasks
or to include the results of earlier learning on the same task
in case the original data are lost but the output of another
learning system is still available.
.
Thus, we see that template functions
could be used for example
to allow transfer of knowledge between similar tasks
or to include the results of earlier learning on the same task
in case the original data are lost but the output of another
learning system is still available.
Including non-zero template functions
generalizes functional 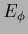 of Eq. (187)
to
of Eq. (187)
to
In the language of physics
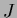 =
= 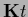 represents an external field
coupling to
represents an external field
coupling to 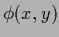 ,
similar, for example, to a magnetic field.
A non-zero field leads to a non-zero expectation of
,
similar, for example, to a magnetic field.
A non-zero field leads to a non-zero expectation of 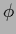 in the no-data case.
The
in the no-data case.
The 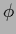 -independent constant
stands for the term
-independent constant
stands for the term
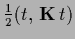 ,
or
,
or
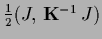 for invertible
for invertible 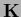 ,
and can be skipped from the error/energy functional
,
and can be skipped from the error/energy functional 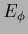 .
.
The stationarity equation for an 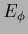 with non-zero
template
with non-zero
template 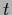 contains an inhomogeneous term
contains an inhomogeneous term
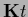 =
= 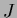
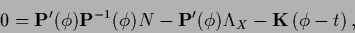 |
(228) |
with, for invertible
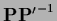 and
and
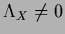 ,
,
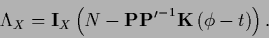 |
(229) |
Notice that functional (226)
can be rewritten as a functional with zero template  in terms of
in terms of
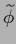 =
= 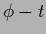 .
That is the reason why we have not included non-zero templates
in the previous sections.
For general non-additive combinations of
squared distances of the form (225)
non-zero templates cannot be removed from the functional
as we will see in Section 6.
Additive combinations of squared error terms,
on the other hand, can again be written as one
squared error term,
using a generalized `bias-variance'-decomposition
.
That is the reason why we have not included non-zero templates
in the previous sections.
For general non-additive combinations of
squared distances of the form (225)
non-zero templates cannot be removed from the functional
as we will see in Section 6.
Additive combinations of squared error terms,
on the other hand, can again be written as one
squared error term,
using a generalized `bias-variance'-decomposition
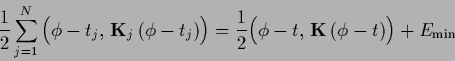 |
(230) |
with template average
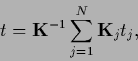 |
(231) |
assuming the existence of the inverse of
the operator
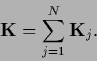 |
(232) |
and minimal energy/error
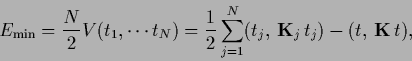 |
(233) |
which up to a factor 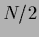 represents a generalized
template variance
represents a generalized
template variance 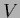 .
We end with the remark that adding error terms
corresponds
in its probabilistic Bayesian interpretation
to ANDing independent events.
For example, if we wish to implement that
.
We end with the remark that adding error terms
corresponds
in its probabilistic Bayesian interpretation
to ANDing independent events.
For example, if we wish to implement that 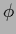 is likely to be smooth AND mirror symmetric,
we may add two squared error terms, one related to smoothness
and another to mirror symmetry.
According to (230) the result will be
a single squared error term of form (225).
is likely to be smooth AND mirror symmetric,
we may add two squared error terms, one related to smoothness
and another to mirror symmetry.
According to (230) the result will be
a single squared error term of form (225).
Summarizing, we have seen
that there are many potentially useful applications
of non-zero template functions.
Technically, however,
non-zero template functions can be removed from the formalism by a simple
substitution
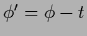 if the error functional consists of
an additive combination of quadratic prior terms.
As most regularized error functionals used in practice have additive
prior terms this is probably the reason that they
are formulated for
if the error functional consists of
an additive combination of quadratic prior terms.
As most regularized error functionals used in practice have additive
prior terms this is probably the reason that they
are formulated for  ,
meaning that non-zero templates functions (base lines)
have to be treated by including a preprocessing step switching
from
,
meaning that non-zero templates functions (base lines)
have to be treated by including a preprocessing step switching
from 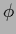 to
to 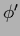 .
We will see in Section 6
that for general error functionals templates cannot be removed
by a simple substitution and do enter the error functionals
explicitly.
.
We will see in Section 6
that for general error functionals templates cannot be removed
by a simple substitution and do enter the error functionals
explicitly.




Next: Quadratic density estimation and
Up: Gaussian prior factors
Previous: Example: Approximate periodicity
Contents
Joerg_Lemm
2001-01-21
![]() measures the squared
measures the squared ![]() -distance
of
-distance
of ![]() to the zero function
to the zero function ![]() .
Choosing a zero mean function for the prior process
is calculationally convenient for Gaussian priors,
but by no means mandatory.
In particular,
a function
.
Choosing a zero mean function for the prior process
is calculationally convenient for Gaussian priors,
but by no means mandatory.
In particular,
a function ![]() is
in practice often measured relative to some non-trivial base line.
Without further a priori information
that base line can in principle be an arbitrary function.
Choosing a zero mean function that base line does not enter
the formulae
and remains hidden in the realization of the measurement process.
On the the other hand,
including explicitly a non-zero mean function
is
in practice often measured relative to some non-trivial base line.
Without further a priori information
that base line can in principle be an arbitrary function.
Choosing a zero mean function that base line does not enter
the formulae
and remains hidden in the realization of the measurement process.
On the the other hand,
including explicitly a non-zero mean function ![]() , playing the role of
a function
, playing the role of
a function
![]() (or reference, target, prototype, base line)
and being technically relatively straightforward,
can be a very powerful tool.
It allows, for example, to
parameterize
(or reference, target, prototype, base line)
and being technically relatively straightforward,
can be a very powerful tool.
It allows, for example, to
parameterize ![]() ) by introducing hyperparameters
(see Section 5)
and to specify explicitly different maxima of multimodal functional priors
(see Section 6.
[132,133,134,135,136]).
All this cannot be done by referring to a single baseline.
) by introducing hyperparameters
(see Section 5)
and to specify explicitly different maxima of multimodal functional priors
(see Section 6.
[132,133,134,135,136]).
All this cannot be done by referring to a single baseline.
![]() of Eq. (187)
to
of Eq. (187)
to
![]() with non-zero
template
with non-zero
template ![]() contains an inhomogeneous term
contains an inhomogeneous term
![]() =
= ![]()
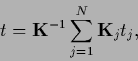
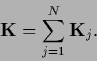
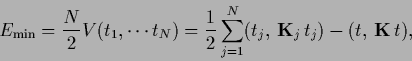
![]() if the error functional consists of
an additive combination of quadratic prior terms.
As most regularized error functionals used in practice have additive
prior terms this is probably the reason that they
are formulated for
if the error functional consists of
an additive combination of quadratic prior terms.
As most regularized error functionals used in practice have additive
prior terms this is probably the reason that they
are formulated for ![]() ,
meaning that non-zero templates functions (base lines)
have to be treated by including a preprocessing step switching
from
,
meaning that non-zero templates functions (base lines)
have to be treated by including a preprocessing step switching
from ![]() to
to ![]() .
We will see in Section 6
that for general error functionals templates cannot be removed
by a simple substitution and do enter the error functionals
explicitly.
.
We will see in Section 6
that for general error functionals templates cannot be removed
by a simple substitution and do enter the error functionals
explicitly.