Often it is more convenient to work with log-probabilities
![]() =
= ![]() than with probabilities.
Firstly,
this ensures non-negativity
of probabilities
than with probabilities.
Firstly,
this ensures non-negativity
of probabilities ![]() =
= ![]() for arbitrary
for arbitrary ![]() .
(For
.
(For ![]() = 0 the log-probability becomes
= 0 the log-probability becomes ![]() =
= ![]() .)
Thus, when working with log-probabilities
one can skip the non-negativity constraint
which would be necessary when working with probabilities.
Secondly,
the multiplication of probabilities for independent events,
yielding their joint probability,
becomes a sum when written in terms of
.)
Thus, when working with log-probabilities
one can skip the non-negativity constraint
which would be necessary when working with probabilities.
Secondly,
the multiplication of probabilities for independent events,
yielding their joint probability,
becomes a sum when written in terms of ![]() .
Indeed,
from
.
Indeed,
from
![]() =
=
![]() =
= ![]() it follows for
it follows for
![]() =
=
![]() that
that
![]() =
=
![]() =
= ![]() .
Especially in the limit where an infinite number of events
is combined by AND,
this would result in
an infinite product for
.
Especially in the limit where an infinite number of events
is combined by AND,
this would result in
an infinite product for ![]() but yields an integral for
but yields an integral for ![]() ,
which is typically easier to treat.
,
which is typically easier to treat.
Besides the requirement of being non-negative,
probabilities have to be normalized,
e.g.,
![]() = 1.
When dealing with a large set of elementary events
normalization is numerically a nontrivial task.
It is then convenient
to work as far as possible with
unnormalized probabilities
= 1.
When dealing with a large set of elementary events
normalization is numerically a nontrivial task.
It is then convenient
to work as far as possible with
unnormalized probabilities ![]() from which normalized probabilities are obtained
as
from which normalized probabilities are obtained
as ![]() =
= ![]() with partition sum
with partition sum ![]() =
=
![]() .
Like for probabilities, it is also often advantageous
to work with the logarithm of unnormalized probabilities,
or to get positive numbers (for
.
Like for probabilities, it is also often advantageous
to work with the logarithm of unnormalized probabilities,
or to get positive numbers (for ![]() )
with the negative logarithm
)
with the negative logarithm
![]() =
=
![]() ,
in physics also known as energy.
(For the role of
,
in physics also known as energy.
(For the role of ![]() see below.)
Similarly,
see below.)
Similarly, ![]() =
=
![]() is known as free energy.
is known as free energy.
Defining the energy we have introduced a parameter ![]() .
Varying the parameter
.
Varying the parameter ![]() generates an exponential family of densities
which is frequently used in practice
by (simulated or deterministic) annealing techniques
for minimizing free energies
[114,156,199,43,1,203,243,68,244,245].
In physics
generates an exponential family of densities
which is frequently used in practice
by (simulated or deterministic) annealing techniques
for minimizing free energies
[114,156,199,43,1,203,243,68,244,245].
In physics ![]() is known as inverse temperature
and plays the role of a Lagrange multiplier
in the maximum entropy approach to statistical physics.
Inverse temperature
is known as inverse temperature
and plays the role of a Lagrange multiplier
in the maximum entropy approach to statistical physics.
Inverse temperature
![]() can also be seen as an external field coupling to the energy.
Indeed, the free energy
can also be seen as an external field coupling to the energy.
Indeed, the free energy
![]() is a generating function for the cumulants of the energy,
meaning that cumulants of
is a generating function for the cumulants of the energy,
meaning that cumulants of ![]() can be obtained by taking derivatives of
can be obtained by taking derivatives of ![]() with respect to
with respect to ![]() [62,9,13,163].
For a detailled discussion
of the relations between probability, log-probability, energy, free energy,
partition sums, generating functions,
and also bit numbers and information see [133].
[62,9,13,163].
For a detailled discussion
of the relations between probability, log-probability, energy, free energy,
partition sums, generating functions,
and also bit numbers and information see [133].
The posterior ![]() , for example, can so be written
as
, for example, can so be written
as
| (4) |
| (5) |
| (6) |
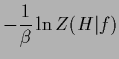 |
(7) | ||
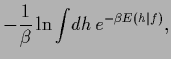 |
(8) |
| (9) | |||
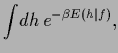 |
(10) |
| (11) |
For the sake of clarity,
we have chosen to use the common notation for conditional probabilities
also for energies and the other quantities derived from them.
The same conventions will also be used for other probabilities,
so we will write for example for likelihoods
In Section 2.3 we will discuss the maximum a posteriori approximation
where an optimal ![]() is found by maximizing the posterior
is found by maximizing the posterior ![]() .
Since maximizing the posterior means minimizing
the posterior energy
.
Since maximizing the posterior means minimizing
the posterior energy ![]() the latter plays the role of an error functional for
the latter plays the role of an error functional for ![]() to be minimized.
This is technically similar to the
minimization of an regularized error functional
as it appears in regularization theory or
empirical risk minimization,
and which is discussed in
Section 2.5.
to be minimized.
This is technically similar to the
minimization of an regularized error functional
as it appears in regularization theory or
empirical risk minimization,
and which is discussed in
Section 2.5.
Let us have a closer look
to the integral over model states ![]() .
The variables
.
The variables ![]() represent the parameters describing
the data generating probabilities or likelihoods
represent the parameters describing
the data generating probabilities or likelihoods
![]() .
In this paper we will mainly be interested in
``nonparametric'' approaches where
the
.
In this paper we will mainly be interested in
``nonparametric'' approaches where
the ![]() -dependent numbers
-dependent numbers ![]() itself are considered to be the primary degrees of freedom
which ``parameterize'' the model states
itself are considered to be the primary degrees of freedom
which ``parameterize'' the model states ![]() .
Then, the integral over
.
Then, the integral over ![]() is an integral over a set of real variables
indexed by
is an integral over a set of real variables
indexed by ![]() ,
, ![]() ,
under additional non-negativity and normalization condition.
,
under additional non-negativity and normalization condition.
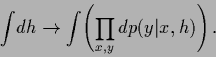 |
(13) |