



Next: Mutual information and learning
Up: Basic model and notations
Previous: Posterior and likelihood
Contents
Within a Bayesian approach predictions
about (e.g., future) events are based
on the predictive probability density,
being the expectation of probability for 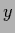 for given (test) situation
for given (test) situation 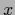 , training data
, training data 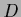 and prior data
and prior data 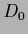
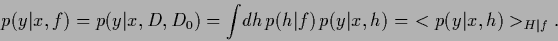 |
(27) |
Here
 denotes the expectation under the posterior
denotes the expectation under the posterior
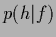 =
= 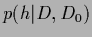 , the state of knowledge
, the state of knowledge 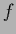 depending on prior and training data.
Successful applications of Bayesian approaches
rely strongly on an adequate choice of the model space
depending on prior and training data.
Successful applications of Bayesian approaches
rely strongly on an adequate choice of the model space 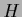 and model likelihoods
and model likelihoods 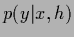 .
.
Note that
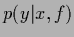 is in the convex cone spanned by the possible states of Nature
is in the convex cone spanned by the possible states of Nature
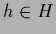 ,
and typically not equal
to one of these
,
and typically not equal
to one of these 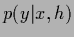 .
The situation is illustrated in Fig. 2.
During learning the predictive density
.
The situation is illustrated in Fig. 2.
During learning the predictive density 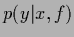 tends to approach the true
tends to approach the true 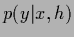 .
Because the training data are random variables,
this approach is stochastic.
(There exists an extensive literature analyzing
the stochastic properties of learning and generalization
from a statistical mechanics perspective
[63,64,65,231,239,178]).
.
Because the training data are random variables,
this approach is stochastic.
(There exists an extensive literature analyzing
the stochastic properties of learning and generalization
from a statistical mechanics perspective
[63,64,65,231,239,178]).
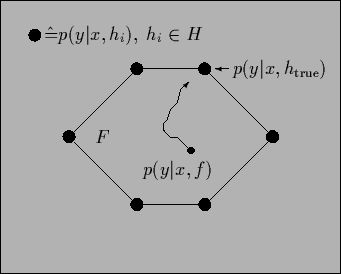
Figure 2:
The predictive density 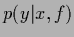 for a state of knowledge
for a state of knowledge 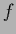 =
= 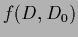 is in the convex hull spanned
by the possible states of Nature
is in the convex hull spanned
by the possible states of Nature 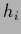 characterized by the likelihoods
characterized by the likelihoods 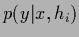 .
During learning the actual predictive density
.
During learning the actual predictive density 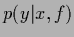 tends to move stochastically towards the extremal point
tends to move stochastically towards the extremal point
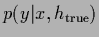 representing the ``true'' state of Nature.
representing the ``true'' state of Nature.
 |




Next: Mutual information and learning
Up: Basic model and notations
Previous: Posterior and likelihood
Contents
Joerg_Lemm
2001-01-21
![]() for given (test) situation
for given (test) situation ![]() , training data
, training data ![]() and prior data
and prior data ![]()
![]() is in the convex cone spanned by the possible states of Nature
is in the convex cone spanned by the possible states of Nature
![]() ,
and typically not equal
to one of these
,
and typically not equal
to one of these ![]() .
The situation is illustrated in Fig. 2.
During learning the predictive density
.
The situation is illustrated in Fig. 2.
During learning the predictive density ![]() tends to approach the true
tends to approach the true ![]() .
Because the training data are random variables,
this approach is stochastic.
(There exists an extensive literature analyzing
the stochastic properties of learning and generalization
from a statistical mechanics perspective
[63,64,65,231,239,178]).
.
Because the training data are random variables,
this approach is stochastic.
(There exists an extensive literature analyzing
the stochastic properties of learning and generalization
from a statistical mechanics perspective
[63,64,65,231,239,178]).
