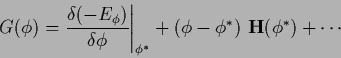Next: Massive relaxation
Up: Learning matrices
Previous: Learning algorithms for density
Contents
For linear equations
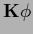 =
=  where
where  and
and 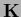 are no functions of
are no functions of 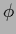 a spectral radius
a spectral radius
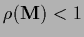 (the largest modulus of the eigenvalues)
of the iteration matrix
(the largest modulus of the eigenvalues)
of the iteration matrix
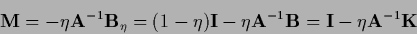 |
(631) |
would guarantee convergence of the iteration scheme.
This is easily seen by solving the linear equation
by iteration according to (615)
A zero mode of 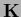 ,
for example a constant function for
differential operators without boundary conditions,
corresponds to an eigenvalue
,
for example a constant function for
differential operators without boundary conditions,
corresponds to an eigenvalue 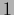 of
of 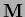 and would lead to divergence of the sequence
and would lead to divergence of the sequence 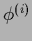 .
However, a nonlinear
.
However, a nonlinear 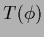 or
or
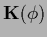 ,
like the nonlinear normalization constraint
contained in
,
like the nonlinear normalization constraint
contained in 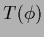 ,
can then still lead to a unique solution.
,
can then still lead to a unique solution.
A convergence analysis for nonlinear equations can be done
in a linear approximation around a fixed point.
Expanding the gradient at 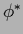
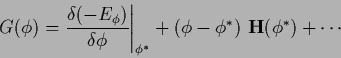 |
(635) |
shows that the factor of the linear term
is the Hessian.
Thus in the vicinity of 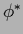 the spectral radius of the iteration matrix
the spectral radius of the iteration matrix
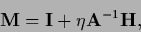 |
(636) |
determines the rate of convergence.
The Newton algorithm uses the negative
Hessian 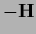 as learning matrix provided it exists
and is positive definite. Otherwise it must resort to other methods.
In the linear approximation (i.e., for quadratic energy)
the Newton algorithm
as learning matrix provided it exists
and is positive definite. Otherwise it must resort to other methods.
In the linear approximation (i.e., for quadratic energy)
the Newton algorithm
is optimal.
We have already seen in Sections 3.1.3 and 3.2.3
that the inhomogeneities
generate in the Hessian in addition to 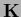 a diagonal part
which can remove zero modes of
a diagonal part
which can remove zero modes of 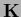 .
.




Next: Massive relaxation
Up: Learning matrices
Previous: Learning algorithms for density
Contents
Joerg_Lemm
2001-01-21
![]() =
= ![]() where
where ![]() and
and ![]() are no functions of
are no functions of ![]() a spectral radius
a spectral radius
![]() (the largest modulus of the eigenvalues)
of the iteration matrix
(the largest modulus of the eigenvalues)
of the iteration matrix
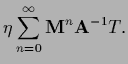
![]()