Next: Inverse Hartree-Fock theory
Up: Inverse many-body theory
Previous: Inverse many-body theory
Contents
In this section the Bayesian approach
for inverse problems will be applied to many-body systems.
To be specific, we will study the simultaneous measurement
of the positions of 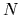 particles.
We assume the measurement result to be given
as a vector
particles.
We assume the measurement result to be given
as a vector 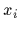 consisting of
consisting of 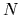 single particle coordinates
single particle coordinates 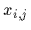 .
The treatment can easily be generalized to partial measurements
of
.
The treatment can easily be generalized to partial measurements
of 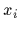 by including an integration over components
which have not been observed.
The likelihood for
by including an integration over components
which have not been observed.
The likelihood for 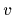 , if measuring a vector
, if measuring a vector 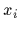 of coordinates,
becomes for a many-body system
of coordinates,
becomes for a many-body system
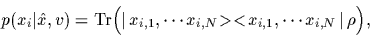 |
(61) |
which is now
a thermal expectation with respect to many-body energies
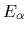
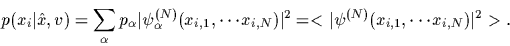 |
(62) |
In particular, we will be interested in fermions
for which the wave functions 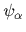 and
and
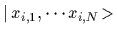 have to be antisymmetric.
Considering a canonical ensemble,
the density operator
have to be antisymmetric.
Considering a canonical ensemble,
the density operator 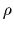 has still the form
of Eq. (15),
but with
has still the form
of Eq. (15),
but with 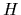 replaced now by a many-body Hamiltonian.
For fermions, it is convenient to express
the many-body Hamiltonian in second quantization,
i.e., in terms of creation and annihilation operators
[76,77].
A Hamiltonian with one-body part
replaced now by a many-body Hamiltonian.
For fermions, it is convenient to express
the many-body Hamiltonian in second quantization,
i.e., in terms of creation and annihilation operators
[76,77].
A Hamiltonian with one-body part 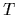 ,
e.g.,
,
e.g., 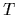 =
= 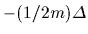 ,
and two-body potential
,
and two-body potential 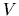 can so be written
can so be written
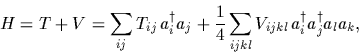 |
(63) |
with antisymmetrized matrix elements 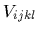 .
Hereby,
.
Hereby,
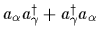 =
=
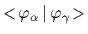 is equal to the overlap
of the one-body orbitals
is equal to the overlap
of the one-body orbitals
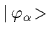 =
=
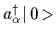 and
and
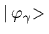 =
=
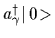 which are created or destroyed
by the operators
which are created or destroyed
by the operators
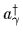 or
or 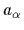 , respectively.
Furthermore,
, respectively.
Furthermore,
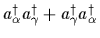 =0,
=0,
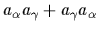 =0.
A two-body eigenfunction of the Hamiltonian (63)
can for example be expanded as follows
=0.
A two-body eigenfunction of the Hamiltonian (63)
can for example be expanded as follows
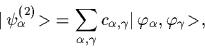 |
(64) |
where
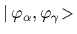 =
=
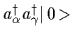 denotes a Slater determinant
being an antisymmetrized wavefunction.
denotes a Slater determinant
being an antisymmetrized wavefunction.
The symmetrized version of a potential,
local in relative coordinates, is
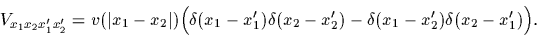 |
(65) |
Here we can always choose 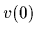 = 0.
Now, assume we are interested in the reconstruction
of
= 0.
Now, assume we are interested in the reconstruction
of 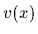 for
for 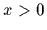 .
Solving the stationarity equation of the
maximum posterior approximation
analogous to Eq. (44) of Sect. 3,
the prior terms remains unchanged
and only the likelihood terms have to be adapted.
Using
.
Solving the stationarity equation of the
maximum posterior approximation
analogous to Eq. (44) of Sect. 3,
the prior terms remains unchanged
and only the likelihood terms have to be adapted.
Using
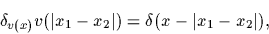 |
(66) |
we find
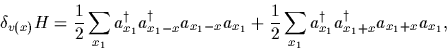 |
(67) |
where 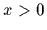 ,
and can write, similar to the one-body case,
,
and can write, similar to the one-body case,
From this the functional derivatives of the likelihoods,
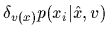 ,
can be obtained. However, a direct numerical or analytical solution
of the full inverse many-body equations
is usually not feasible.
To deal with this problem,
a mean field approach
will be developed in the next section.
,
can be obtained. However, a direct numerical or analytical solution
of the full inverse many-body equations
is usually not feasible.
To deal with this problem,
a mean field approach
will be developed in the next section.




Next: Inverse Hartree-Fock theory
Up: Inverse many-body theory
Previous: Inverse many-body theory
Contents
Joerg_Lemm
2000-06-06
![]() particles.
We assume the measurement result to be given
as a vector
particles.
We assume the measurement result to be given
as a vector ![]() consisting of
consisting of ![]() single particle coordinates
single particle coordinates ![]() .
The treatment can easily be generalized to partial measurements
of
.
The treatment can easily be generalized to partial measurements
of ![]() by including an integration over components
which have not been observed.
The likelihood for
by including an integration over components
which have not been observed.
The likelihood for ![]() , if measuring a vector
, if measuring a vector ![]() of coordinates,
becomes for a many-body system
of coordinates,
becomes for a many-body system