



Next: Integer hyperparameters
Up: Parameterizing priors: Hyperparameters
Previous: Regularization parameters
Contents
In the previous sections we have studied saddle point approximations
which lead us to maximize the joint posterior
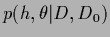 simultaneously with respect to the hidden variables
simultaneously with respect to the hidden variables 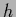 and
and 
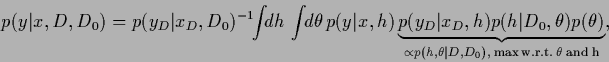 |
(486) |
assuming for the maximization with respect to 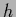 a slowly varying
a slowly varying 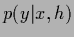 at the stationary point.
at the stationary point.
This simultaneous maximization with respect to both variables
is consistent with the usual asymptotic
justification of a saddle point approximation.
For example, for a function 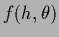 of two
(for example, one-dimensional)
variables
of two
(for example, one-dimensional)
variables 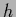 ,
, 
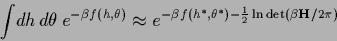 |
(487) |
for large enough 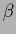 (and a unique maximum).
Here
(and a unique maximum).
Here
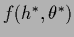 denotes the joint minimum
and
denotes the joint minimum
and 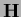 the Hessian of
the Hessian of 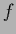 with respect to
with respect to 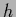 and
and  .
For
.
For  -dependent determinant of the covariance
and the usual definition of
-dependent determinant of the covariance
and the usual definition of 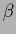 ,
results in a function
,
results in a function 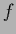 of the form
of the form
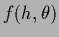 =
=
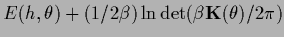 ,
where both terms are relevant for
the minimization of
,
where both terms are relevant for
the minimization of 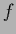 with respect to
with respect to  .
For large
.
For large 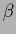 , however, the second term
becomes small compared to the first one.
(Of course, there is the possibility that a saddle point approximation
is not adequate for the
, however, the second term
becomes small compared to the first one.
(Of course, there is the possibility that a saddle point approximation
is not adequate for the  integration.
Also, we have seen
that the condition of a positive definite covariance
may lead to a solution for
integration.
Also, we have seen
that the condition of a positive definite covariance
may lead to a solution for  on the boundary
where the (unrestricted) stationarity equation is not fulfilled.)
on the boundary
where the (unrestricted) stationarity equation is not fulfilled.)
Alternatively,
one might think of performing the two integrals stepwise.
This seems especially useful if one integral
can be calculated analytically.
Consider, for example
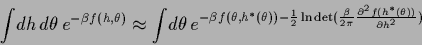 |
(488) |
which would be exact for a Gaussian 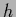 -integral.
One sees now that
minimizing the complete negative exponent
-integral.
One sees now that
minimizing the complete negative exponent
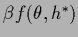 +
+
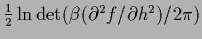 with respect to
with respect to  is different from minimizing only
is different from minimizing only 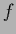 in (487),
if the second derivative of
in (487),
if the second derivative of 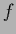 with respect to
with respect to 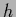 depends on
depends on  (which is not the case for a Gaussian
(which is not the case for a Gaussian  integral).
Again this additional term becomes negligible for large enough
integral).
Again this additional term becomes negligible for large enough 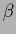 .
Thus, at least asymptotically,
this term may be altered or even be skipped,
and differences in the results of
the variants of saddle point approximation
will be expected to be small.
.
Thus, at least asymptotically,
this term may be altered or even be skipped,
and differences in the results of
the variants of saddle point approximation
will be expected to be small.
Stepwise approaches like (488) can be used, for example
to perform Gaussian integrations analytically,
and lead to somewhat simpler
stationarity equations for  -dependent covariances
[236].
-dependent covariances
[236].
In particular,
let us look at
the case of Gaussian regression in a bit more detail.
The following discussion, however, also applies
to density estimation if, as in (488),
the Gaussian first step integration is replaced
by a saddle point approximation including the normalization factor.
(This requires the calculation of the determinant of the Hessian.)
Consider the two step procedure for Gaussian regression
where in a first step
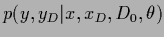 can be calculated
analytically and in a second step the
can be calculated
analytically and in a second step the  integral is performed
by Gaussian approximation around a stationary point.
Instead of maximizing
the joint posterior
integral is performed
by Gaussian approximation around a stationary point.
Instead of maximizing
the joint posterior
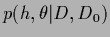 with respect to
with respect to 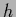 and
and  this approach performs the
this approach performs the 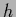 -integration analytically and maximizes
-integration analytically and maximizes
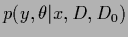 with respect to
with respect to  .
The disadvantage of this approach
is the
.
The disadvantage of this approach
is the 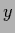 -, and
-, and 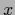 -dependency of the resulting solution.
-dependency of the resulting solution.
Thus,
assuming a slowly varying
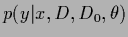 at the stationary point
it appears simpler to
maximize the
at the stationary point
it appears simpler to
maximize the 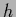 -marginalized
posterior,
-marginalized
posterior,
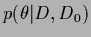 =
=
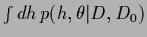 ,
if the
,
if the 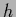 -integration can be performed exactly,
-integration can be performed exactly,
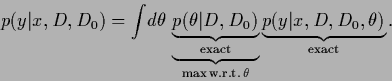 |
(490) |
Having found a maximum posterior solution 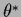 the corresponding analytical solution
for
the corresponding analytical solution
for
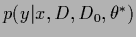 is then given by Eq. (321).
The posterior density
is then given by Eq. (321).
The posterior density
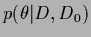 can be obtained from the likelihood of
can be obtained from the likelihood of  and a specified prior
and a specified prior 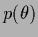
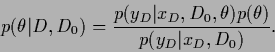 |
(491) |
Thus, in case the  -likelihood can be calculated
analytically,
the
-likelihood can be calculated
analytically,
the  -integral is calculated in saddle point approximation
by maximizing the posterior for
-integral is calculated in saddle point approximation
by maximizing the posterior for  with respect to
with respect to  .
In the case of a uniform
.
In the case of a uniform 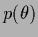 the optimal
the optimal 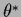 is obtained
by maximizing the
is obtained
by maximizing the  -likelihood.
This corresponds technically to an empirical Bayes approach
[35].
As
-likelihood.
This corresponds technically to an empirical Bayes approach
[35].
As 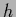 is integrated out in
is integrated out in
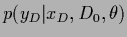 the
the  -likelihood is also called
marginalized likelihood.
-likelihood is also called
marginalized likelihood.
Indeed, for Gaussian regression,
the  -likelihood
can be integrated analytically.
Analogously to Section 3.7.2 one finds
[228,237,236],
-likelihood
can be integrated analytically.
Analogously to Section 3.7.2 one finds
[228,237,236],
where
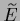 =
=
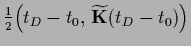 ,
,
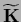 =
=
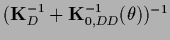 =
=
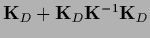 ,
,
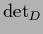 the determinant in data space,
and we used that
from
the determinant in data space,
and we used that
from
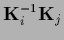 =
= 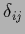 for
for 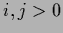 follows
follows
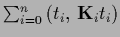 =
=
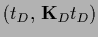 +
+
 =
=
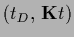 ,
with
,
with
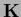 =
=
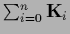 .
In cases where the marginalization over
.
In cases where the marginalization over 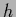 ,
necessary to obtain the evidence,
cannot be performed analytically
and all
,
necessary to obtain the evidence,
cannot be performed analytically
and all 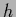 -integrals are calculated in saddle point approximation,
we get the same result as
for a direct simultaneous MAP for
-integrals are calculated in saddle point approximation,
we get the same result as
for a direct simultaneous MAP for 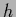 and
and  for the predictive density
as indicated in (486).
for the predictive density
as indicated in (486).
Now we are able to compare the three
resulting stationary equations for
 -dependent mean
-dependent mean 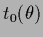 ,
inverse covariance
,
inverse covariance
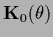 and prior
and prior 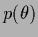 .
Setting the derivative of the joint posterior
.
Setting the derivative of the joint posterior
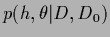 with respect to
with respect to  to zero yields
to zero yields
This equation which we have already discussed
has to be solved simultaneously with the stationarity equation
for 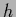 .
While this approach is easily adapted
to general density estimation problems,
its difficulty for
.
While this approach is easily adapted
to general density estimation problems,
its difficulty for  -dependent covariance determinants
lies in calculation of the derivative of the determinant of
-dependent covariance determinants
lies in calculation of the derivative of the determinant of 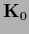 .
Maximizing the
.
Maximizing the 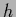 -marginalized posterior
-marginalized posterior
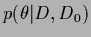 ,
on the other hand,
only requires
the calculation of the derivative of the determinant of the
,
on the other hand,
only requires
the calculation of the derivative of the determinant of the
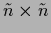 matrix
matrix
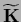
Evaluated
at the stationary
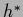 =
=
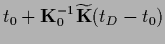 ,
the first term of Eq. (493),
which does not contain derivatives of the inverse covariances,
becomes equal to the first term of Eq. (494).
The last terms of
Eqs. (493) and (494)
are always identical.
Typically, the data-independent
,
the first term of Eq. (493),
which does not contain derivatives of the inverse covariances,
becomes equal to the first term of Eq. (494).
The last terms of
Eqs. (493) and (494)
are always identical.
Typically, the data-independent 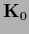 has a more regular structure
than the data-dependent
has a more regular structure
than the data-dependent
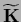 .
Thus,
at least for one or two dimensional
.
Thus,
at least for one or two dimensional 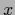 ,
a straightforward numerical solution of Eq. (493)
by discretizing
,
a straightforward numerical solution of Eq. (493)
by discretizing 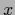 can also be a good choice for Gaussian regression problems.
can also be a good choice for Gaussian regression problems.
Analogously, from Eq. (321) follows
for maximizing
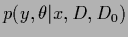 with respect to
with respect to 
which is 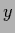 -, and
-, and 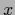 -dependent.
Such an approach may be considered
if interested only in specific test data
-dependent.
Such an approach may be considered
if interested only in specific test data 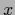 ,
, 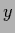 .
.
We may remark that also in Gaussian regression the  -integral
may be quite different from a Gaussian integral,
so a saddle point approximation
does not necessarily have to give satisfactory results.
In cases one encounters problems one can, for example, try
variable transformations
-integral
may be quite different from a Gaussian integral,
so a saddle point approximation
does not necessarily have to give satisfactory results.
In cases one encounters problems one can, for example, try
variable transformations
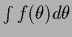 =
=
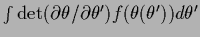 to obtain a more Gaussian shape of the integrand.
Due to the presence of the Jacobian determinant, however,
the asymptotic interpretation of the corresponding saddle point approximation
is different for the two integrals.
The variability of saddle point approximations
results from the freedom to add terms which vanish
asymptotically but remains finite in the nonasymptotic region.
Similar effects are known in quantum many body theory
(see for example [172], chapter 7.)
Alternatively, the
to obtain a more Gaussian shape of the integrand.
Due to the presence of the Jacobian determinant, however,
the asymptotic interpretation of the corresponding saddle point approximation
is different for the two integrals.
The variability of saddle point approximations
results from the freedom to add terms which vanish
asymptotically but remains finite in the nonasymptotic region.
Similar effects are known in quantum many body theory
(see for example [172], chapter 7.)
Alternatively, the  -integral can be solved numerically
by Monte Carlo methods[237,236].
-integral can be solved numerically
by Monte Carlo methods[237,236].




Next: Integer hyperparameters
Up: Parameterizing priors: Hyperparameters
Previous: Regularization parameters
Contents
Joerg_Lemm
2001-01-21
![]() simultaneously with respect to the hidden variables
simultaneously with respect to the hidden variables ![]() and
and ![]()
![]() of two
(for example, one-dimensional)
variables
of two
(for example, one-dimensional)
variables ![]() ,
, ![]()
![]() -dependent covariances
[236].
-dependent covariances
[236].
![]() at the stationary point
it appears simpler to
maximize the
at the stationary point
it appears simpler to
maximize the ![]() -marginalized
posterior,
-marginalized
posterior,
![]() =
=
![]() ,
if the
,
if the ![]() -integration can be performed exactly,
-integration can be performed exactly,
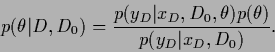
![]() -likelihood
can be integrated analytically.
Analogously to Section 3.7.2 one finds
[228,237,236],
-likelihood
can be integrated analytically.
Analogously to Section 3.7.2 one finds
[228,237,236],
![]() -dependent mean
-dependent mean ![]() ,
inverse covariance
,
inverse covariance
![]() and prior
and prior ![]() .
Setting the derivative of the joint posterior
.
Setting the derivative of the joint posterior
![]() with respect to
with respect to ![]() to zero yields
to zero yields
![]() with respect to
with respect to ![]()
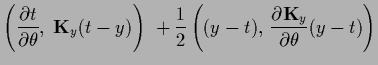
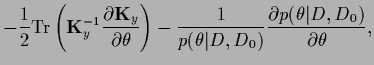
![]() -integral
may be quite different from a Gaussian integral,
so a saddle point approximation
does not necessarily have to give satisfactory results.
In cases one encounters problems one can, for example, try
variable transformations
-integral
may be quite different from a Gaussian integral,
so a saddle point approximation
does not necessarily have to give satisfactory results.
In cases one encounters problems one can, for example, try
variable transformations
![]() =
=
![]() to obtain a more Gaussian shape of the integrand.
Due to the presence of the Jacobian determinant, however,
the asymptotic interpretation of the corresponding saddle point approximation
is different for the two integrals.
The variability of saddle point approximations
results from the freedom to add terms which vanish
asymptotically but remains finite in the nonasymptotic region.
Similar effects are known in quantum many body theory
(see for example [172], chapter 7.)
Alternatively, the
to obtain a more Gaussian shape of the integrand.
Due to the presence of the Jacobian determinant, however,
the asymptotic interpretation of the corresponding saddle point approximation
is different for the two integrals.
The variability of saddle point approximations
results from the freedom to add terms which vanish
asymptotically but remains finite in the nonasymptotic region.
Similar effects are known in quantum many body theory
(see for example [172], chapter 7.)
Alternatively, the ![]() -integral can be solved numerically
by Monte Carlo methods[237,236].
-integral can be solved numerically
by Monte Carlo methods[237,236].