



Nächste Seite: Berechnung von
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Die optimale Hedging-Strategie
Inhalt
In Abschnitt 3.1
hatten das Prinzip der minimalen Varianz
[Gl. (12)] vorgestellt
um eine optimale Hedging-Strategie  zu bestimmen,
zu bestimmen,
![\begin{displaymath}
\phi^* = {\rm argmin}_\phi <\left[\Delta_\rho W_N(\phi)\right]^2\!>
.
\end{displaymath}](img78.gif) |
(71) |
Für den Fall einer Call-Option ergibt sich,
wobei  kollektiv diejenigen Terme bezeichnet,
die unabhängig sind von
kollektiv diejenigen Terme bezeichnet,
die unabhängig sind von  .
.
Für den ersten  -abhängigen Term
in Gl. (72) erhalten wir
unter der Annahme unabhängiger
-abhängigen Term
in Gl. (72) erhalten wir
unter der Annahme unabhängiger
 ,
,
da weder  noch
noch
 von
von
 mit
mit  abhängen und
aufgrund der Normierung von Wahrscheinlichkeiten,
abhängen und
aufgrund der Normierung von Wahrscheinlichkeiten,
 |
(74) |
Mit
 |
(75) |
läßt sich auch schreiben,
 |
(76) |
Für den zweiten  -abhängigen Term
in Gl. (72) ist es nützlich
die Kursentwicklung von
-abhängigen Term
in Gl. (72) ist es nützlich
die Kursentwicklung von
 in die drei Abschnitte
in die drei Abschnitte
 ,
,
 und
und
 zu zerlegen
(Physiker mögen sich dabei an die Berechnung von
Erwartungswerten mit Pfadintegralen erinnert fühlen),
zu zerlegen
(Physiker mögen sich dabei an die Berechnung von
Erwartungswerten mit Pfadintegralen erinnert fühlen),
Hierbei ist
 =
=
 , also
die Wahrscheinlichkeit für
, also
die Wahrscheinlichkeit für  zum Zeitpunkt
zum Zeitpunkt  .
Analog sind
.
Analog sind
 sowie
sowie
 Spezialfälle der allgemeinen Definition,
Spezialfälle der allgemeinen Definition,
 |
(78) |
die Wahrscheinlichkeit von  zur Zeit
zur Zeit  nach
nach 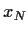 zur Zeit
zur Zeit  zu gelangen.
Insbesondere ist
zu gelangen.
Insbesondere ist  also noch von
also noch von  abhängig.
Es gilt
abhängig.
Es gilt
 |
(79) |
Weiterhin bezeichnet
 |
(80) |
den Mittelwert von
 über alle Pfade, die von
über alle Pfade, die von  nach
nach 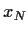 gehen,
gewichted mit
gehen,
gewichted mit  .
Diese Größe kann also ungleich Null sein
selbst wenn
.
Diese Größe kann also ungleich Null sein
selbst wenn
 = 0.
= 0.




Nächste Seite: Berechnung von
Aufwärts: Die optimale Hedging-Strategie
Vorherige Seite: Die optimale Hedging-Strategie
Inhalt
Joerg_Lemm
2000-02-02
![]() zu bestimmen,
zu bestimmen,
![]() -abhängigen Term
in Gl. (72) erhalten wir
unter der Annahme unabhängiger
-abhängigen Term
in Gl. (72) erhalten wir
unter der Annahme unabhängiger
![]() ,
,
![$\displaystyle \int\left( \prod_{m=0}^{N-1} d(\Delta_\rho x_m) p(\Delta_\rho x_m)\right)
\left[\phi_k(x_k)\right]^2 \left[\Delta_\rho x_k\right]^2$](img311.gif)
![$\displaystyle \underbrace{
\left(
\int\left( \prod_{m=0}^{k-1} d(\Delta_\rho x_...
...,\left[\Delta_\rho x_k\right]^2
\right)
}_{\displaystyle <(\Delta_\rho x_k)^2>}$](img312.gif)


![]() -abhängigen Term
in Gl. (72) ist es nützlich
die Kursentwicklung von
-abhängigen Term
in Gl. (72) ist es nützlich
die Kursentwicklung von
![]() in die drei Abschnitte
in die drei Abschnitte
![]() ,
,
![]() und
und
![]() zu zerlegen
(Physiker mögen sich dabei an die Berechnung von
Erwartungswerten mit Pfadintegralen erinnert fühlen),
zu zerlegen
(Physiker mögen sich dabei an die Berechnung von
Erwartungswerten mit Pfadintegralen erinnert fühlen),

![% latex2html id marker 4275
$\displaystyle \underbrace{
\int\left( \prod_{m=0}^{...
...splaystyle
\int \!dx_k p(x_k\vert x_0) \phi_k
\;\mbox{[Gl. (\ref{defP})]}
}$](img326.gif)
![% latex2html id marker 4276
$\displaystyle \times
\underbrace{
\int \! d(\Delta_...
...!dx_{k+1} p(x_{k+1}\vert x_k) \Delta_\rho x_k
\;\mbox{[Gl. (\ref{defP})]}
}$](img327.gif)
![% latex2html id marker 4277
$\displaystyle \times
\underbrace{
\int\left( \prod_...
...^\infty \!dx_N p(x_N\vert x_{k+1}) (x_N-x_s)
\;\mbox{[Gl. (\ref{defP})]}
}$](img328.gif)

![% latex2html id marker 4281
$\displaystyle \int \!dx_k p(x_k\vert x_0) \phi_...
...a_\rho x_k\!>_{x_k\rightarrow x_N}
\;\mbox{[Gln. (\ref{kolmo}, \ref{mean2})]}
}$](img330.gif)

![]() =
=
![]() , also
die Wahrscheinlichkeit für
, also
die Wahrscheinlichkeit für ![]() zum Zeitpunkt
zum Zeitpunkt ![]() .
Analog sind
.
Analog sind
![]() sowie
sowie
![]() Spezialfälle der allgemeinen Definition,
Spezialfälle der allgemeinen Definition,