



Nächste Seite: Vermögensbilanz bei Optionsgeschäften
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Der ``faire'' Preis einer
Inhalt
Erwartungswertprinzip und ``No-Arbitrage''-Prinzip
Ist ein Handel mit dem Underlying
eines Termingeschäftes nicht möglich, so
ergibt sich aus einem
Anfangsvermögen
 zur Zeit
zur Zeit  für ein Termingeschäft mit der Vermögenswirkung
für ein Termingeschäft mit der Vermögenswirkung
 zur Zeit
zur Zeit  ein Gesamtvermögen
ein Gesamtvermögen  =
=  zur Zeit
zur Zeit  von
von
 |
(1) |
Für ein Forward hatten wir beispielsweise gesehen,
daß für den Halter der Short-Position
 |
(2) |
wobei  =
=  den Kaufpreis representiert zu dem der Halter
der Short-Position sich zur Zeit
den Kaufpreis representiert zu dem der Halter
der Short-Position sich zur Zeit  verpflichtet hat
das Underlying zur Zeit
verpflichtet hat
das Underlying zur Zeit  zu kaufen.
Die Variable
zu kaufen.
Die Variable 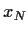 bezeichnet den tatsächlichen Preis
des Underlyings der sich zur Zeit
bezeichnet den tatsächlichen Preis
des Underlyings der sich zur Zeit  ergeben hat.
Nehmen wir für risikolose Anleihen
eine Zinsrate an von
ergeben hat.
Nehmen wir für risikolose Anleihen
eine Zinsrate an von  für die Zeit
für die Zeit  =
=  ,
so ergibt sich nach
,
so ergibt sich nach  Zeitschritten
Zeitschritten
 |
(3) |
mit  =
=  bei konstantem
bei konstantem
 =
=  =
=  .
Eine naheliegende Bedingung an einen fairen Preis
ist die Forderung, daß keine Partei
durch das Termingeschäft bevorzugt oder benachteiligt werden soll.
Dies bedeuted das
das Vermögen
.
Eine naheliegende Bedingung an einen fairen Preis
ist die Forderung, daß keine Partei
durch das Termingeschäft bevorzugt oder benachteiligt werden soll.
Dies bedeuted das
das Vermögen  zur zeit
zur zeit 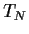 nicht durch Abschluß des Geschäftes
beinflußt werden darf, also
nicht durch Abschluß des Geschäftes
beinflußt werden darf, also
 |
(4) |
wobei
 dasjenige Vermögen darstellt,
was sich ohne Termingeschäft zur Zeit
dasjenige Vermögen darstellt,
was sich ohne Termingeschäft zur Zeit 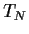 ergäben hätte.
Für den (unrealistischen) Fall eines Forwards
auf ein Underlying mit deterministischer Zeitentwicklung
ergäbe sich beispielsweise das triviale Resultat,
ergäben hätte.
Für den (unrealistischen) Fall eines Forwards
auf ein Underlying mit deterministischer Zeitentwicklung
ergäbe sich beispielsweise das triviale Resultat,
 |
(5) |
Typischerweise
ist 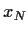 jedoch eine Zufallsgröße.
Dann führt die Forderung, daß keine Partei im Mittel
bevorzugt oder benachteiligt werden soll, zu,
jedoch eine Zufallsgröße.
Dann führt die Forderung, daß keine Partei im Mittel
bevorzugt oder benachteiligt werden soll, zu,
 |
(6) |
Im Falle eines Forwards folgt also
 |
(7) |
Diese Methode einen Preis für ein Termingeschäft zu berechnen
nennt sich deshalb Erwartungswertprinzip (Bachelier).
Sobald das Underlying aber handelbar ist,
kann sich die Situation wesentlich verändern.
Beschränken wir uns auf den Handel mit dem Underlying
des betrachteten Termingeschäftes, so können wir eine Handelstrategie
kennzeichnen durch die Anzahl  der zur Zeit
der zur Zeit  gehaltenen Underlyinganteile zum momentanen Preis von
gehaltenen Underlyinganteile zum momentanen Preis von  .
Bezieht man den Gewinn bzw. Verlust aus dem Handel mit dem Underlying
in die Vermögensbilanz mit ein,
so verallgemeinert sich Gl. (1) zu,
.
Bezieht man den Gewinn bzw. Verlust aus dem Handel mit dem Underlying
in die Vermögensbilanz mit ein,
so verallgemeinert sich Gl. (1) zu,
 |
(8) |
Den Gewinn bzw. Verlust
aus dem Handel mit dem Underlying
haben wir bereits im
Kapitel über unbedingte Termingeschäfte berechnet,
^{N-k-1}
,
\end{displaymath}](img65.gif) |
(9) |
bezogen auf die Zeit  und
mit diskontierten (auf
und
mit diskontierten (auf  abgezinsten)
abgezinsten)
 =
=
 .
Verschiedene Handelstrategien
.
Verschiedene Handelstrategien
 =
=
 führen jetzt im allgemeinen zu einer unterschiedlichen Verteilung
führen jetzt im allgemeinen zu einer unterschiedlichen Verteilung
 .
Die Veränderung des Vermögens
.
Die Veränderung des Vermögens
 im Zeitraum
im Zeitraum  enthält zwei Zufallsanteile,
nämlich
enthält zwei Zufallsanteile,
nämlich
Zur Bestimmung eines Preises für ein Termingeschäft
müssen wir uns also als erstes auf eine (Hedging-)Strategie  festlegen.
Ähnlich zu unserem Vorgehen bei Portfolio-Optimierung
besteht nun eine Möglichkeit darin
auf das Prinzip der minimalen Varianz zurückzugreifen.
In diesem Falle verstehen wir als optimale Strategie
dasjenige
festlegen.
Ähnlich zu unserem Vorgehen bei Portfolio-Optimierung
besteht nun eine Möglichkeit darin
auf das Prinzip der minimalen Varianz zurückzugreifen.
In diesem Falle verstehen wir als optimale Strategie
dasjenige  , welches
die Varianz der Vermögensänderung minimiert,
, welches
die Varianz der Vermögensänderung minimiert,
![\begin{displaymath}
\phi^* = {\rm argmin}_\phi <\left[\Delta_\rho W_N(\phi)\right]^2\!>
.
\end{displaymath}](img78.gif) |
(12) |
Anstatt den Erwartungswert wie bei der Portfolio-Optimierung zu fixieren,
können wir ihn nun zur Bestimmung eines fairen Preis verwenden
indem wir fordern,
 |
(13) |
also
 |
(14) |
Üblicherweise nehmen wir an, daß die Akteure
keine marktbeherschende Stellung einnehmen, d.h.,
daß die Handelstrategie  den Preis
den Preis 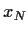 nicht beeinflußt,
also
nicht beeinflußt,
also
 .
.
Im Falle eines Forward
fanden wir
 |
(15) |
(wobei  =
=  ,
,
 =
=  ,
,
 =
=  und
und
 = 0,
= 0,
 = 0),
also
= 0),
also
 |
(16) |
Damit ist also bei der Wahl
 die Varianz
die Varianz
![$<\left[\Delta_\rho W_N(\phi)\right]^2\!>$](img90.gif) = 0,
so daß
= 0,
so daß
 |
(17) |
Wir haben bereits diskutiert,
daß
für den Fall
der Handelbarkeit des Underlyings,
sich dieser Preis einstellen muß da eine Abweichung davon
risikolose Gewinne (Arbitrage)
möglich macht.
In solch einem risikolosen Fall spricht man vom
``No-Arbitrage''-Prinzip zur Preisbestimmung
eines Termingeschäftes.
Im Falle von Optionen ist eine Handelsstrategie,
die eine Streuungsfreie Vermögensbilanz
zur Zeit  liefert nur unter idealisierten
Bedingungen möglich, auf denen z.B.
der klassische Black-Scholes-Ansatz beruht.
liefert nur unter idealisierten
Bedingungen möglich, auf denen z.B.
der klassische Black-Scholes-Ansatz beruht.
Im allgemeinen Fall, wenn keine Hedging-Strategie  mit verschwindender Varianz
mit verschwindender Varianz
![$<\left[\Delta_\rho W_N(\phi^*)\right]^2\!>$](img92.gif) = 0
möglich ist, wird der Verkäufer
eine Risikoprämie
= 0
möglich ist, wird der Verkäufer
eine Risikoprämie
 zu dem
aus der Forderung
zu dem
aus der Forderung
 bestimmten
Preis
bestimmten
Preis
 addieren.
Als Gesamtpreis einer Option
addieren.
Als Gesamtpreis einer Option
 ergibt sich dann,
ergibt sich dann,
 |
(18) |




Nächste Seite: Vermögensbilanz bei Optionsgeschäften
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Der ``faire'' Preis einer
Inhalt
Joerg_Lemm
2000-02-02
![]() zur Zeit
zur Zeit ![]() für ein Termingeschäft mit der Vermögenswirkung
für ein Termingeschäft mit der Vermögenswirkung
![]() zur Zeit
zur Zeit ![]() ein Gesamtvermögen
ein Gesamtvermögen ![]() =
= ![]() zur Zeit
zur Zeit ![]() von
von
![]() der zur Zeit
der zur Zeit ![]() gehaltenen Underlyinganteile zum momentanen Preis von
gehaltenen Underlyinganteile zum momentanen Preis von ![]() .
Bezieht man den Gewinn bzw. Verlust aus dem Handel mit dem Underlying
in die Vermögensbilanz mit ein,
so verallgemeinert sich Gl. (1) zu,
.
Bezieht man den Gewinn bzw. Verlust aus dem Handel mit dem Underlying
in die Vermögensbilanz mit ein,
so verallgemeinert sich Gl. (1) zu,
^{N-k-1}
,
\end{displaymath}](img65.gif)
![]() liefert nur unter idealisierten
Bedingungen möglich, auf denen z.B.
der klassische Black-Scholes-Ansatz beruht.
liefert nur unter idealisierten
Bedingungen möglich, auf denen z.B.
der klassische Black-Scholes-Ansatz beruht.
![]() mit verschwindender Varianz
mit verschwindender Varianz
![]() = 0
möglich ist, wird der Verkäufer
eine Risikoprämie
= 0
möglich ist, wird der Verkäufer
eine Risikoprämie
![]() zu dem
aus der Forderung
zu dem
aus der Forderung
![]() bestimmten
Preis
bestimmten
Preis
![]() addieren.
Als Gesamtpreis einer Option
addieren.
Als Gesamtpreis einer Option
![]() ergibt sich dann,
ergibt sich dann,