



Nächste Seite: Der Fall = 0
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Vermögensbilanz bei Optionsgeschäften
Inhalt
Da wir im Folgenden spezeill den Fall
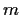 = 0 näher diskutieren wollen,
schätzen wir den Einfluß von
= 0 näher diskutieren wollen,
schätzen wir den Einfluß von 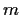 auf den Optionspreis ab.
Wir berechnen dazu den Erwartungswert
auf den Optionspreis ab.
Wir berechnen dazu den Erwartungswert
 |
(33) |
für eine ``At the money''-Option, d.h.,
für  =
=  .
Da eine normale und log-normale Verteilung
in ihrem zentralen Bereich gut übereinstimmen,
wählen wir eine Gaußverteilung für
die Differenz
.
Da eine normale und log-normale Verteilung
in ihrem zentralen Bereich gut übereinstimmen,
wählen wir eine Gaußverteilung für
die Differenz  mit Mittelwert
mit Mittelwert  und Varianz
und Varianz
 =
=
 .
(Unter der Annahme
.
(Unter der Annahme
 =
=
 gilt
gilt
 =
=
 ).
Wir erhalten für
).
Wir erhalten für  =
=  ,
,
mit  =
=  ,
,
 =
=
 .
Hierbei haben wir benutzt, daß
.
Hierbei haben wir benutzt, daß
 |
(35) |
sowie
![\begin{displaymath}
\frac{1}{\sqrt{2\pi}}\int_a^\infty \!dz e^{-\frac{z^2}{2}}
=
\frac{1}{2} \left[1-{\rm erf}(\frac{a}{\sqrt{2}})\right]
.
\end{displaymath}](img173.gif) |
(36) |
Schließlich haben wir bis zur ersten Ordnung in  entwickelt gemäß
entwickelt gemäß
und angenommen, daß
 |
(40) |
ist (also  ).
).
Bei  = 100 Tagen,
einer Tagesvolatilität von
= 100 Tagen,
einer Tagesvolatilität von  = 1%,
einer durchschnittlichen jährlichen Rendite
von
= 1%,
einer durchschnittlichen jährlichen Rendite
von 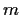 = 5%
und einem Underlyingkurs von
= 5%
und einem Underlyingkurs von  = 100 Punkten,
erhalten wir
= 100 Punkten,
erhalten wir
 |
(41) |
Resultate für
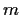 = 0 können also
eine sinnvolle erste Näherung sein.
Insbesondere ist die klassische Black-Scholes-Lösung
= 0 können also
eine sinnvolle erste Näherung sein.
Insbesondere ist die klassische Black-Scholes-Lösung
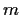 -unabhängig.
-unabhängig.




Nächste Seite: Der Fall = 0
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Vermögensbilanz bei Optionsgeschäften
Inhalt
Joerg_Lemm
2000-02-02
![]() = 0 näher diskutieren wollen,
schätzen wir den Einfluß von
= 0 näher diskutieren wollen,
schätzen wir den Einfluß von ![]() auf den Optionspreis ab.
Wir berechnen dazu den Erwartungswert
auf den Optionspreis ab.
Wir berechnen dazu den Erwartungswert


![$\displaystyle \sqrt{\frac{DT}{2\pi}}
e^{-\frac{\left(\frac{mT}{\sqrt{DT}}\right)^2}{2}}
+\frac{mT}{2} \left[1-{\rm erf}(-\frac{mT}{\sqrt{2DT}})\right]$](img162.gif)
![$\displaystyle \sqrt{\frac{DT}{2\pi}}
+\frac{mT}{2} [1+\frac{\sqrt{2}}{\sqrt{\pi}} \frac{mT}{\sqrt{DT}}]$](img165.gif)

![]() = 100 Tagen,
einer Tagesvolatilität von
= 100 Tagen,
einer Tagesvolatilität von ![]() = 1%,
einer durchschnittlichen jährlichen Rendite
von
= 1%,
einer durchschnittlichen jährlichen Rendite
von ![]() = 5%
und einem Underlyingkurs von
= 5%
und einem Underlyingkurs von ![]() = 100 Punkten,
erhalten wir
= 100 Punkten,
erhalten wir
