


Next: Nonlinear constraints and spin
Up: Capital Asset Pricing Model
Previous: Capital Asset Pricing Model
Equation (37) follows also from
predicting 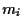 from
from 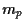 by a linear regression model.
Specifically, assume
by a linear regression model.
Specifically, assume 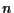 data pairs
data pairs
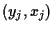 .
In the case of the CAPM these data will be pairs
.
In the case of the CAPM these data will be pairs
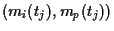 ,
sampled for example at times
,
sampled for example at times 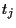 .
Out aim is to find an optimal prediction of the
.
Out aim is to find an optimal prediction of the
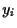 based on the
based on the 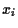 (i.e.,, for CAPM, prediction of
the
(i.e.,, for CAPM, prediction of
the 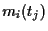 based on the
based on the 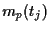 ).
To determine an optimal predicting function
).
To determine an optimal predicting function
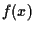 we define a quadratic error measure
we define a quadratic error measure
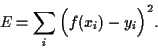 |
(40) |
In the particular situation of linear regression
the function 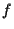 is linear,
is linear, 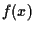 =
=
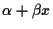 .
(A more flexible
.
(A more flexible 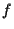 would for example be a neural network.)
The optimal parameters
would for example be a neural network.)
The optimal parameters 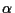 ,
, 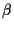 are now found as usual by setting
are now found as usual by setting
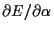 = 0 and
= 0 and
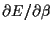 = 0.
Thus,
= 0.
Thus,
or
from which follows
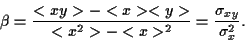 |
(45) |
The definition of 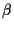 being thus the same,
Eq. (43)
can now be identified with
Eq. (37) with
being thus the same,
Eq. (43)
can now be identified with
Eq. (37) with
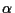 corresponding to
corresponding to 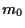 ,
,
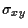 to
to 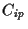 ,
and
,
and 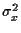 to
to 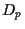 .
.



Next: Nonlinear constraints and spin
Up: Capital Asset Pricing Model
Previous: Capital Asset Pricing Model
Joerg_Lemm
2000-02-25
![]() from
from ![]() by a linear regression model.
Specifically, assume
by a linear regression model.
Specifically, assume ![]() data pairs
data pairs
![]() .
In the case of the CAPM these data will be pairs
.
In the case of the CAPM these data will be pairs
![]() ,
sampled for example at times
,
sampled for example at times ![]() .
Out aim is to find an optimal prediction of the
.
Out aim is to find an optimal prediction of the
![]() based on the
based on the ![]() (i.e.,, for CAPM, prediction of
the
(i.e.,, for CAPM, prediction of
the ![]() based on the
based on the ![]() ).
To determine an optimal predicting function
).
To determine an optimal predicting function
![]() we define a quadratic error measure
we define a quadratic error measure