As a first numerical application we discuss the reconstruction of a
one-dimensional periodic potential.
For example, such a potential may represent a
one-dimensional solid surface.
To be specific, assume we expect the potential to be periodic,
or even more, to be similar
to a certain periodic reference potential ![]() .
However, we do not want to restrict the approximation to a parametric form
but want to keep the approximating potential flexible,
so it can adapt to arbitrary deviations from
the periodic reference potential as indicated by the data.
For example, such deviations may be caused by impurities on
an otherwise regular surface.
Assuming the deviations from the reference
to be smooth on a scale defined by
.
However, we do not want to restrict the approximation to a parametric form
but want to keep the approximating potential flexible,
so it can adapt to arbitrary deviations from
the periodic reference potential as indicated by the data.
For example, such deviations may be caused by impurities on
an otherwise regular surface.
Assuming the deviations from the reference
to be smooth on a scale defined by ![]() ,
these assumptions can be implemented by a Gaussian smoothness prior
with mean
,
these assumptions can be implemented by a Gaussian smoothness prior
with mean ![]() , and, say, Laplacian inverse covariance.
Including the likelihood terms for the empirical data,
and possibly a term
, and, say, Laplacian inverse covariance.
Including the likelihood terms for the empirical data,
and possibly a term ![]() adapting the average energy,
we end up with an error functional (negative log-posterior)
to be minimized
adapting the average energy,
we end up with an error functional (negative log-posterior)
to be minimized
 |
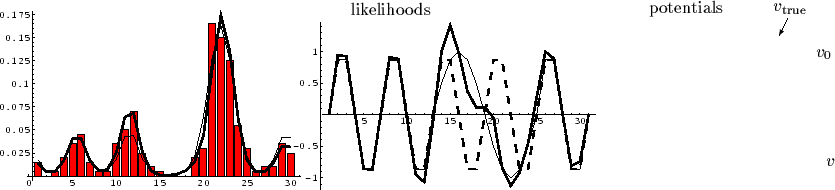 |
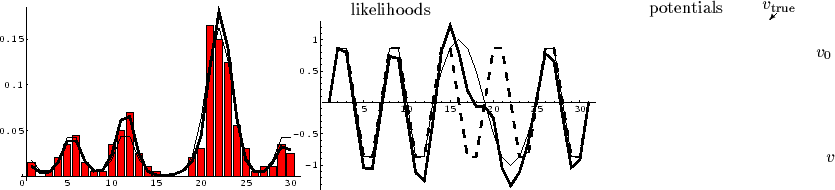
Fig. 2 shows representative examples
of numerical results
for functional (51)
without energy penalty term ![]() and
with a periodic reference potential (dashed line),
and
with a periodic reference potential (dashed line),
![]() =
= ![]() ,
on a one-dimensional grid with 30 points.
Data have been sampled according to a likelihood
function derived from
a `true' or original potential
,
on a one-dimensional grid with 30 points.
Data have been sampled according to a likelihood
function derived from
a `true' or original potential ![]() (shown as thin line)
under periodic boundary conditions for
(shown as thin line)
under periodic boundary conditions for ![]() .
The reconstructed potential (thick line)
has been obtained by minimizing
Eq. (51)
iterating according to Eq. (49)
with
.
The reconstructed potential (thick line)
has been obtained by minimizing
Eq. (51)
iterating according to Eq. (49)
with ![]() =
=
![]() and zero boundary conditions for
and zero boundary conditions for ![]() (so
(so ![]() is invertible)
and initial guess
is invertible)
and initial guess ![]() =
= ![]() .
.
Notice, that the distortion of the underlying `true' potential has been clearly identified. On the other hand the reconstructed potential coincides well with the periodic reference potential at locations where supported by data.
We want to stress two phenomena
which are typical for the reconstruction of potentials
from empirical data and can also be seen in the figures.
Firstly, the approximation of the likelihood
function is usually better than the approximation
of the potential.
This is due to the fact that quite different potentials
can produce similar likelihoods.
This emphasizes
the relevance of a priori information
for reconstructing potentials.
Secondly,
especially in low data regions, i.e., at high potentials,
the potential is not well determined.
Thus, empirical data mainly contribute
to the approximation of regions with low potential,
while a priori information
becomes especially important in regions
where the potential is large.
More data will can be obtained for high potential regions
when the temperature is increased
which spreads the data over a wider area.
At the same time, however, the likelihood becomes more uniform
at large temperatures, making an identification of ![]() more difficult.
more difficult.
Because the reference potential ![]() has the same average energy
has the same average energy ![]() as the underlying original potential
the results are already reasonable
without energy penalty term
as the underlying original potential
the results are already reasonable
without energy penalty term ![]() .
Indeed,
Fig. 3
shows the relatively small influence of an additional
energy penalty term with quite large
.
Indeed,
Fig. 3
shows the relatively small influence of an additional
energy penalty term with quite large ![]() on the likelihood function.
Thus, the approximated probability for empirical data is not much altered.
The presence of an
on the likelihood function.
Thus, the approximated probability for empirical data is not much altered.
The presence of an ![]() term is better visible for the potential.
In particular its minima
fit now better that of the original.
In the next section, where we will work with a zero reference
potential
term is better visible for the potential.
In particular its minima
fit now better that of the original.
In the next section, where we will work with a zero reference
potential ![]() , the energy penalty term
, the energy penalty term ![]() will be more important.
will be more important.