



Next: Classical approximation
Up: Numerical case studies in
Previous: Approximately periodic potentials
Contents
As a second example we study the reconstruction of a two-body potential
by measuring inter-particle distances 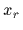 .
Consider the
two-body problem
.
Consider the
two-body problem
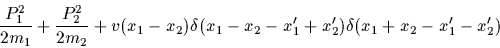 |
(52) |
with single particle momenta 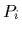 =
=
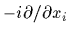 .
The problem is transformed to a one-body problem
in the relative coordinates
in the usual way by introducing
i.e.,
.
The problem is transformed to a one-body problem
in the relative coordinates
in the usual way by introducing
i.e.,
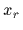 =
= 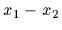 ,
,
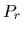 =
=
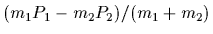 ,
,
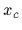 =
=
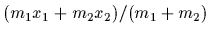 ,
,
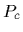 =
= 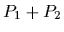 ,
,
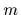 =
=
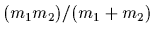 ,
and
,
and 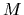 =
= 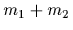 resulting in
resulting in
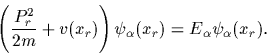 |
(53) |
The total energy is additive
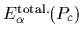 =
=
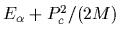 so the thermal probabilities
so the thermal probabilities 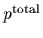 factorize
and integrating out the center of mass motion leaves
factorize
and integrating out the center of mass motion leaves
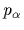 =
=
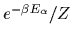 ,
with
,
with 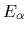 being the eigenvalues of Eq. (53).
being the eigenvalues of Eq. (53).
Figure 4:
Approximation of symmetric potential.
Shown are likelihoods (left hand side)
and potentials (right hand side):
Original likelihood and potential (thin lines),
approximated likelihood and potential (thick lines),
empirical density (bars),
The parameters used are:
20 data points for a particle with 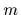 = 0.1,
truncated RBF covariances
as in Eq. (54) with
= 0.1,
truncated RBF covariances
as in Eq. (54) with
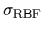 =
= 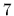 ,
,
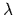 =
= 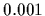 ,
energy penalty term
,
energy penalty term 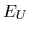 with
with
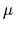 = 20
and reference value
= 20
and reference value 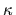 =
= 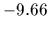 =
=
 (average energy
(average energy 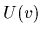 =
= 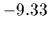 for the approximated
for the approximated 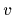 ,
ground state energy
,
ground state energy 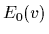 =
= 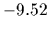 )
inverse physical temperature
)
inverse physical temperature 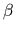 = 1,
and a potential fulfilling
= 1,
and a potential fulfilling
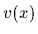 =
= 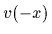 and
and
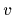 = 0 at the boundaries.
= 0 at the boundaries.
 |
Figure 5:
Same data and parameter
as for Fig. 4
with the exception of
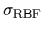 =
= 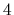 ,
that means with a smaller smoothness constraint,
and
,
that means with a smaller smoothness constraint,
and 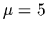 .
(
.
(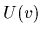 =
= 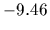 .)
To allow an easier comparison with the reconstructed likelihood
the figure shows the symmetrized empirical density
.)
To allow an easier comparison with the reconstructed likelihood
the figure shows the symmetrized empirical density
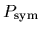 =
=
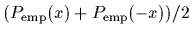 .
.
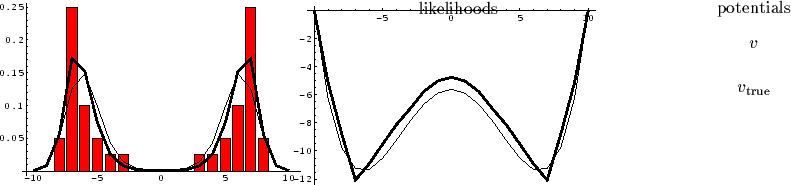 |
Figure 6:
Same data and parameter
as for Fig. 5
but with even smaller smoothness constraint
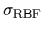 =
= 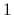 .
(
.
(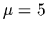 , empirical density symmetrized,
, empirical density symmetrized,
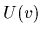 =
= 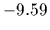 .)
Compared with Figs. 4 and 5,
the empirical density is better approximated
but not the original potential and its likelihood function.
.)
Compared with Figs. 4 and 5,
the empirical density is better approximated
but not the original potential and its likelihood function.
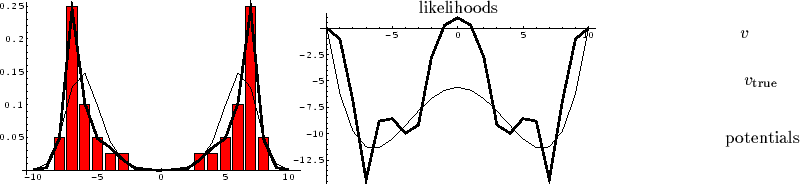 |
Figs. 4 - 6
show typical results
for the numerical
reconstruction of a
one-dimensional,
strictly symmetric potential,
fulfilling 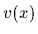 =
= 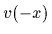 and set to zero at the boundaries.
Training data
have been sampled from a `true' likelihood function
(thin lines),
resulting in an empirical density
and set to zero at the boundaries.
Training data
have been sampled from a `true' likelihood function
(thin lines),
resulting in an empirical density
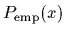 =
= 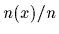 (shown by bars),
where
(shown by bars),
where 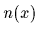 denotes the number of times the value
denotes the number of times the value 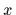 occurs in the training data.
The `true' likelihood has been
constructed from a `true' potential (thin lines)
choosing periodic boundary conditions for the wavefunctions.
In contrast to Sect. 3.3.1
a zero reference potential
occurs in the training data.
The `true' likelihood has been
constructed from a `true' potential (thin lines)
choosing periodic boundary conditions for the wavefunctions.
In contrast to Sect. 3.3.1
a zero reference potential 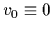 and
a truncated Radial Basis Function (RBF) prior [32]
has been used
and
a truncated Radial Basis Function (RBF) prior [32]
has been used
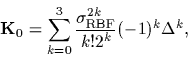 |
(54) |
(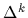 denoting the
denoting the 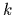 th iterated Laplacian)
which includes, compared to a Laplacian prior,
higher derivatives, hence producing
a rounder reconstructed potential
(cmp. Sect. 3.2.2).
The approximated potentials (thick lines) have been obtained
by iterating Eq. (49), including a term
th iterated Laplacian)
which includes, compared to a Laplacian prior,
higher derivatives, hence producing
a rounder reconstructed potential
(cmp. Sect. 3.2.2).
The approximated potentials (thick lines) have been obtained
by iterating Eq. (49), including a term 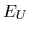 adapting the thermal energy average to that of the original potential.
As iteration matrix we used
adapting the thermal energy average to that of the original potential.
As iteration matrix we used 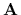 =
=
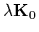 together with an adaptive step size
together with an adaptive step size 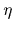 .
An initial guess for the potential
has been obtained by adding negative
.
An initial guess for the potential
has been obtained by adding negative
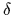 -peaks on the data points (except for data on the boundary), i.e.,
-peaks on the data points (except for data on the boundary), i.e.,
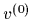 =
=
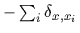 .
The number of iterations necessary to obtain convergence
has been typically between 50 and 100.
.
The number of iterations necessary to obtain convergence
has been typically between 50 and 100.
Comparing Figs. 4 - 6
one sees that a smaller smoothness leads to a better fit
of the empirical density.
A larger smoothness, on the other hand,
leads to better fit in regions where
smoothness is an adequate prior.
Near the boundaries, however,
where the original is relatively steep,
a higher smoothness leads
to a poorer approximation.
A remedy would be, for example,
an adapted reference potential 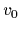 .
.
Figure 7:
Approximation of symmetric potential
with mixture of Gaussian process priors.
The left hand side shows likelihoods
and the right hand side potentials:
Original likelihood and potential (thin lines),
approximated likelihood and potential (thick lines),
symmetrized
empirical density (bars),
and the two reference potentials 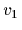 ,
,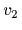 (dashed,
(dashed, 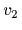 deeper in the middle).
The parameters used are:
20 data points for a particle with
deeper in the middle).
The parameters used are:
20 data points for a particle with 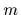 = 0.1,
inverse physical temperature
= 0.1,
inverse physical temperature 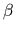 = 1,
= 1,
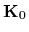 =
= 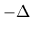 ,
inverse mixture temperature
,
inverse mixture temperature 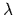 = 0.1,
energy penalty factor
= 0.1,
energy penalty factor 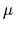 = 10
for average energy
= 10
for average energy 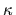 =
= 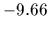 =
=
 (and
(and 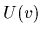 =
= 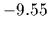 ,
, 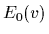 =
= 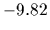 )
)
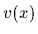 =
= 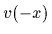 symmetric,
and
symmetric,
and
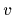 = 0 at the boundaries.
Because the data support both reference potentials
= 0 at the boundaries.
Because the data support both reference potentials
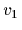 and
and 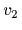 ,
the approximated
,
the approximated 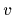 is in regions with no data essentially
a smoothed mixture between
is in regions with no data essentially
a smoothed mixture between 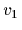 and
and 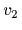 with mixture coefficients for prior components
with mixture coefficients for prior components
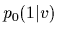 = 0.3,
= 0.3, 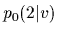 = 0.7.
= 0.7.
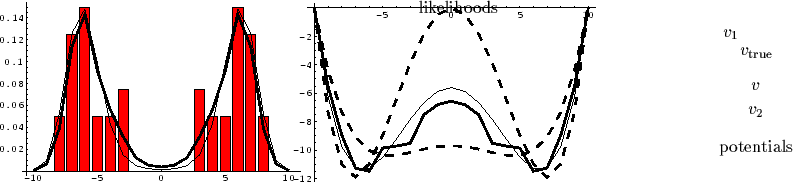 |
Fig. 7
presents an application of a mixture of Gaussian process priors
as given in Eq. (40).
Such mixture priors
can in principle be used to construct
an arbitrary prior density,
adapted to the situation under study.
For the numerical example a two component mixture has been chosen
with equal component variances
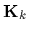 =
= 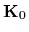 of the form of Eq. (54)
and two reference potentials
of the form of Eq. (54)
and two reference potentials 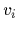 (shown as dashed lines)
with the same average energy
(shown as dashed lines)
with the same average energy 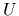 .
In the special situation shown in the figure
both reference functions
.
In the special situation shown in the figure
both reference functions 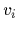 fit similarly well to the empirical data.
(The final mixture coefficients for
fit similarly well to the empirical data.
(The final mixture coefficients for 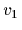 and
and 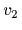 are
are 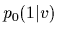 = 0.3 and
= 0.3 and 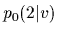 = 0.7.)
Hence, in the no-data region
the approximated potential
= 0.7.)
Hence, in the no-data region
the approximated potential 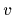 becomes a smoothed, weighted average of
becomes a smoothed, weighted average of 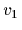 and
and 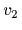 .
Because both reference potentials coincide
also relatively well with the original
.
Because both reference potentials coincide
also relatively well with the original 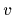 near the boundaries,
the approximation in Fig. 7
is better than in Figs. 4 - 6.
near the boundaries,
the approximation in Fig. 7
is better than in Figs. 4 - 6.
In conclusion, the two one-dimensional examples show
that a direct numerical solution
of the presented Bayesian approach to inverse quantum theory
can be feasible.




Next: Classical approximation
Up: Numerical case studies in
Previous: Approximately periodic potentials
Contents
Joerg_Lemm
2000-06-06
![]() .
Consider the
two-body problem
.
Consider the
two-body problem



![]() =
= ![]() and set to zero at the boundaries.
Training data
have been sampled from a `true' likelihood function
(thin lines),
resulting in an empirical density
and set to zero at the boundaries.
Training data
have been sampled from a `true' likelihood function
(thin lines),
resulting in an empirical density
![]() =
= ![]() (shown by bars),
where
(shown by bars),
where ![]() denotes the number of times the value
denotes the number of times the value ![]() occurs in the training data.
The `true' likelihood has been
constructed from a `true' potential (thin lines)
choosing periodic boundary conditions for the wavefunctions.
In contrast to Sect. 3.3.1
a zero reference potential
occurs in the training data.
The `true' likelihood has been
constructed from a `true' potential (thin lines)
choosing periodic boundary conditions for the wavefunctions.
In contrast to Sect. 3.3.1
a zero reference potential ![]() and
a truncated Radial Basis Function (RBF) prior [32]
has been used
and
a truncated Radial Basis Function (RBF) prior [32]
has been used
![]() .
.

![]() =
= ![]() of the form of Eq. (54)
and two reference potentials
of the form of Eq. (54)
and two reference potentials ![]() (shown as dashed lines)
with the same average energy
(shown as dashed lines)
with the same average energy ![]() .
In the special situation shown in the figure
both reference functions
.
In the special situation shown in the figure
both reference functions ![]() fit similarly well to the empirical data.
(The final mixture coefficients for
fit similarly well to the empirical data.
(The final mixture coefficients for ![]() and
and ![]() are
are ![]() = 0.3 and
= 0.3 and ![]() = 0.7.)
Hence, in the no-data region
the approximated potential
= 0.7.)
Hence, in the no-data region
the approximated potential ![]() becomes a smoothed, weighted average of
becomes a smoothed, weighted average of ![]() and
and ![]() .
Because both reference potentials coincide
also relatively well with the original
.
Because both reference potentials coincide
also relatively well with the original ![]() near the boundaries,
the approximation in Fig. 7
is better than in Figs. 4 - 6.
near the boundaries,
the approximation in Fig. 7
is better than in Figs. 4 - 6.