



Next: General loss functions and
Up: Bayesian decision theory
Previous: Loss and risk
Contents
Loss functions for approximation
Log-loss:
A typical loss function for density estimation problems
is the log-loss
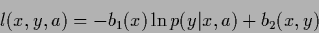 |
(46) |
with some 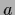 -independent
-independent 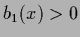 ,
, 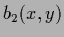 and
actions
and
actions 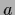 describing probability densities
describing probability densities
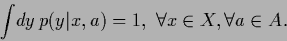 |
(47) |
Choosing  =
= 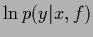 and
and 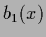 =
= 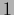 gives
gives
which shows that minimizing log-loss is equivalent to minimizing
the (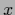 -averaged) Kullback-Leibler entropy
-averaged) Kullback-Leibler entropy
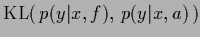 [122,123,13,46,53].
[122,123,13,46,53].
While the paper will concentrate on log-loss
we will also give a short summary of loss functions
for regression problems.
(See for example [16,201] for details.)
Regression problems are special density estimation problems
where the considered possible actions are restricted to
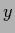 -independent functions
-independent functions 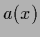 .
.
Squared-error loss:
The most common loss function for regression problems
(see Sections 3.7, 3.7.2)
is the squared-error loss. It reads
for one-dimensional 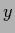
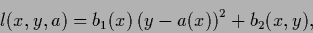 |
(51) |
with arbitrary 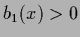 and
and 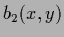 .
In that case the optimal function
.
In that case the optimal function 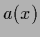 is
the regression function of the posterior
which is the mean of the predictive density
is
the regression function of the posterior
which is the mean of the predictive density
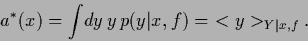 |
(52) |
This can be easily seen by writing
where the first term in (54) is independent of 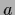 and the last term vanishes after integration over
and the last term vanishes after integration over 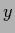 according to the definition of
according to the definition of 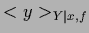 .
Hence,
.
Hence,
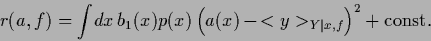 |
(55) |
This is minimized by
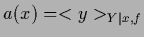 .
Notice that for Gaussian
.
Notice that for Gaussian 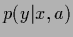 with fixed variance
log-loss and squared-error loss are equivalent.
For multi-dimensional
with fixed variance
log-loss and squared-error loss are equivalent.
For multi-dimensional  one-dimensional loss functions like Eq. (51)
can be used
when the component index of
one-dimensional loss functions like Eq. (51)
can be used
when the component index of  is considered part of the
is considered part of the 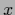 -variables.
Alternatively, loss functions depending explicitly on multidimensional
-variables.
Alternatively, loss functions depending explicitly on multidimensional 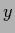 can be defined.
For instance, a general quadratic loss function would be
can be defined.
For instance, a general quadratic loss function would be
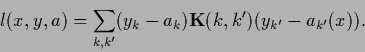 |
(56) |
with symmetric, positive definite kernel
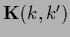 .
.
Absolute loss:
For absolute loss
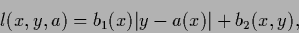 |
(57) |
with arbitrary 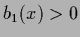 and
and 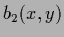 .
The risk becomes
.
The risk becomes
where the integrals have been rewritten as
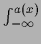 =
=
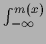 +
+
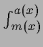 and
and
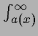 =
=
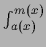 +
+
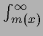 introducing a median function
introducing a median function 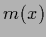 which satisfies
which satisfies
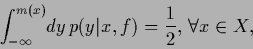 |
(60) |
so that
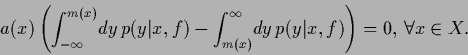 |
(61) |
Thus the risk is minimized by any median function 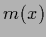 .
.
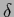 -loss and
-loss and 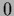 -
-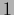 loss :
Another possible loss function,
typical for classification tasks
(see Section 3.8),
like for example image segmentation
[153],
is
the
loss :
Another possible loss function,
typical for classification tasks
(see Section 3.8),
like for example image segmentation
[153],
is
the 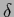 -loss for continuous
-loss for continuous 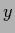 or
or 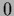 -
-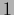 -loss for discrete
-loss for discrete 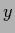
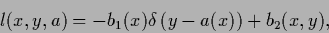 |
(62) |
with arbitrary 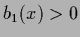 and
and 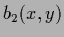 .
Here
.
Here 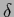 denotes
the Dirac
denotes
the Dirac 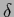 -functional
for continuous
-functional
for continuous 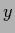 and the Kronecker
and the Kronecker 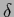 for discrete
for discrete 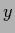 .
Then,
.
Then,
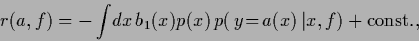 |
(63) |
so the optimal 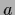 corresponds to any mode function
of the predictive density.
For Gaussians mode and median are unique,
and coincide with the mean.
corresponds to any mode function
of the predictive density.
For Gaussians mode and median are unique,
and coincide with the mean.




Next: General loss functions and
Up: Bayesian decision theory
Previous: Loss and risk
Contents
Joerg_Lemm
2001-01-21
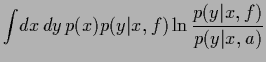
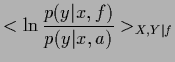
![]() -independent functions
-independent functions ![]() .
.
![]()
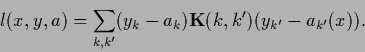
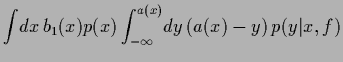
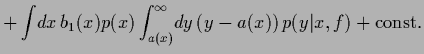
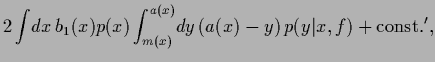
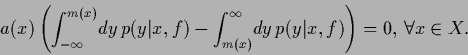
![]() -loss and
-loss and ![]() -
-![]() loss :
Another possible loss function,
typical for classification tasks
(see Section 3.8),
like for example image segmentation
[153],
is
the
loss :
Another possible loss function,
typical for classification tasks
(see Section 3.8),
like for example image segmentation
[153],
is
the ![]() -loss for continuous
-loss for continuous ![]() or
or ![]() -
-![]() -loss for discrete
-loss for discrete ![]()