



Next: Non-Gaussian prior factors
Up: Parameterizing priors: Hyperparameters
Previous: Integer hyperparameters
Contents
Local hyperfields
Most, but not all hyperparameters 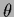 considered so far have been real or integer numbers,
or vectors with real or integer components
considered so far have been real or integer numbers,
or vectors with real or integer components 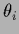 .
With the unrestricted template functions of Sect. 5.2.3
or the functions parameterizing the inverse covariance
in Section 5.3.3,
we have, however, also already encountered
function hyperparameters or hyperfields.
In this section we will now discuss
function hyperparameters in more detail.
.
With the unrestricted template functions of Sect. 5.2.3
or the functions parameterizing the inverse covariance
in Section 5.3.3,
we have, however, also already encountered
function hyperparameters or hyperfields.
In this section we will now discuss
function hyperparameters in more detail.
Functions can be seen as continuous vectors,
the function values 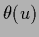 being the (continuous) analogue of vector components
being the (continuous) analogue of vector components 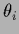 .
In numerical calculations, in particular,
functions usually have to be discretized,
so, numerically, functions stand for high dimensional vectors.
.
In numerical calculations, in particular,
functions usually have to be discretized,
so, numerically, functions stand for high dimensional vectors.
Typical arguments of function hyperparameters
are the independent variables 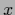 and, for general density estimation, also the dependent variables
and, for general density estimation, also the dependent variables 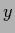 .
Such functions
.
Such functions 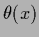 or
or 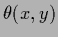 will be called
local hyperparameters or local hyperfields.
Local hyperfields
will be called
local hyperparameters or local hyperfields.
Local hyperfields 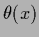 can be used, for example,
to adapt templates or inverse covariances locally.
(For general density estimation problems
replace here and in the following
can be used, for example,
to adapt templates or inverse covariances locally.
(For general density estimation problems
replace here and in the following 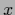 by
by 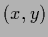 .)
.)
The price to be paid for the additional flexibility
of function hyperparameters
is a large number of additional degrees of freedom.
This can considerably complicate calculations and,
requires a sufficient number of training data
and/or a sufficiently restrictive hyperprior
to be able to determine the hyperfield
and not to make the prior useless.
To introduce local hyperparameters 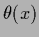 we express real symmetric, positive (semi-)definite inverse covariances
by square roots or ``filter operators''
we express real symmetric, positive (semi-)definite inverse covariances
by square roots or ``filter operators'' 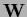 ,
,
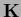 =
=
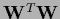 =
=
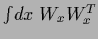 where
where
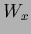 represents the vector
represents the vector
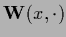 .
Thus, in components
.
Thus, in components
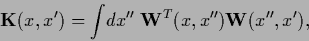 |
(498) |
and therefore
where we defined the ``filtered differences''
![\begin{displaymath}
\omega (x)
=
\big( \, W_x\, ,\, \phi-t \, \big)
=
\int \!dx^\prime \, {\bf W}(x,x^\prime)
[\phi(x^\prime)-t(x^\prime )]
.
\end{displaymath}](img1751.png) |
(500) |
Thus, for a Gaussian prior for 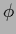 we have
we have
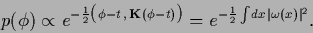 |
(501) |
A real local hyperfield
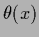 mixing, for instance,
locally two alternative filtered differences
may now be introduced as follows
mixing, for instance,
locally two alternative filtered differences
may now be introduced as follows
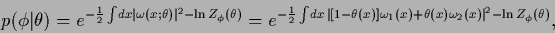 |
(502) |
where
![\begin{displaymath}
\omega (x;\theta)
= [1-\theta(x)] \, \omega_1(x) + \theta(x) \,\omega_2(x)
,
\end{displaymath}](img1754.png) |
(503) |
and, say,
![$\theta(x)\in [0,1]$](img1755.png) .
For unrestricted real
.
For unrestricted real 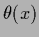 an arbitrary real
an arbitrary real
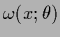 can be obtained.
For a binary local hyperfield
with
can be obtained.
For a binary local hyperfield
with
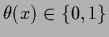 we have
we have
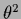 =
= 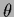 ,
,
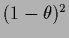 =
= 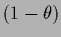 ,
and
,
and
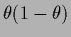 =
= 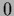 ,
so
Eq. (502)
becomes
,
so
Eq. (502)
becomes
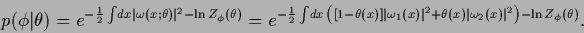 |
(504) |
For real 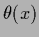 in Eq. (503)
terms with
in Eq. (503)
terms with 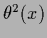 ,
,
![$[1-\theta(x)]^2$](img1764.png) , and
, and
![$[1-\theta(x)]\theta(x)$](img1765.png) would appear in Eq. (504).
A binary
would appear in Eq. (504).
A binary 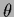 variable can
be obtained from a real
variable can
be obtained from a real
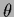 with the help of a step function
with the help of a step function 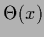 and a threshold
and a threshold 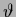 by replacing
by replacing
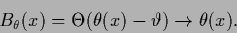 |
(505) |
Clearly, if both prior and hyperprior are formulated
in terms of such 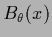 this is equivalent to using directly a binary hyperfield.
this is equivalent to using directly a binary hyperfield.
For a local hyperfield 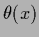 a local adaption of the functions
a local adaption of the functions
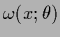 as in Eq. (503)
can be achieved by switching
locally between alternative templates
or alternative filter operators
as in Eq. (503)
can be achieved by switching
locally between alternative templates
or alternative filter operators 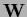
In Eq. (506)
it is important to notice that ``local'' templates
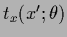 for fixed
for fixed 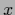 are still functions
of an
are still functions
of an 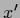 variable.
Indeed, to obtain
variable.
Indeed, to obtain
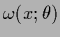 ,
the function
,
the function 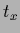 is needed for all
is needed for all 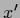 for which
for which 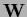 has nonzero entries,
has nonzero entries,
![\begin{displaymath}
\omega(x;\theta )
=
\int\!dx^\prime\,
{\bf W}(x,x^\prime)
[\phi(x^\prime)-t_x(x^\prime;\theta)]
.
\end{displaymath}](img1777.png) |
(508) |
That means that the template
is adapted individually for every local filtered difference.
Thus, Eq. (506)
has to be distinguished from the choice
![\begin{displaymath}
t(x^\prime;\theta)
=
[1-\theta(x^\prime )] \, t_{1}(x^\prime)
+ \theta(x^\prime )\, t_{2}(x^\prime)
.
\end{displaymath}](img1778.png) |
(509) |
The unrestricted adaption of templates
discussed in Sect. 5.2.3,
for instance,
can be seen as an approach of the form of
Eq. (509)
with an unbounded real hyperfield 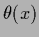 .
.
Eq. (507)
corresponds
for binary 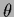 to an inverse covariance
to an inverse covariance
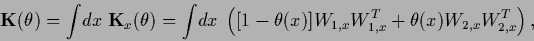 |
(510) |
where
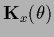 =
=
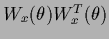 and
and
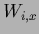 =
=
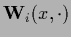 ,
,
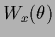 =
=
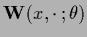 .
We remark that
.
We remark that 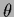 -dependent inverse covariances
require to include the normalization factors
when integrating over
-dependent inverse covariances
require to include the normalization factors
when integrating over 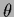 or
solving for the optimal
or
solving for the optimal 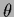 in MAP.
If we consider
two binary hyperfields
in MAP.
If we consider
two binary hyperfields 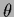 ,
, 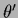 ,
one for
,
one for 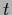 and one for
and one for 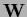 ,
we get a prior
,
we get a prior
![\begin{displaymath}
p(\phi\vert\theta,\theta^\prime)
\propto
e^{-\frac{1}{2}
\in...
...theta)]\big)
}
\propto
e^{-E(\phi\vert\theta,\theta^\prime)}
.
\end{displaymath}](img1787.png) |
(511) |
Up to a 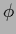 -independent constant
(which still depends on
-independent constant
(which still depends on 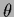 ,
, 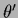 )
the corresponding prior energy
can again be written in the form
)
the corresponding prior energy
can again be written in the form
![\begin{displaymath}
E(\phi\vert\theta,\theta^\prime)
=
\frac{1}{2}
\Big( \phi-t(...
...{\bf K}(\theta^\prime ) [\phi-t(\theta,\theta^\prime)] \Big)
.
\end{displaymath}](img1788.png) |
(512) |
Indeed,
the corresponding effective template
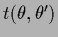 and effective inverse covariance
and effective inverse covariance
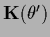 are according to Eqs. (247,252)
given by
are according to Eqs. (247,252)
given by
Hence, one may rewrite
The MAP solution of Gaussian regression
for a prior corresponding to (515)
at optimal 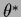 ,
,
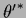 is according to Section 3.7
therefore
given by
is according to Section 3.7
therefore
given by
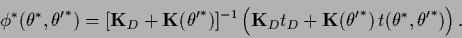 |
(516) |
One may avoid dealing with
``local'' templates 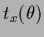 by adapting templates
in prior terms where
by adapting templates
in prior terms where 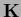 is equal to the identity
is equal to the identity 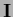 .
In that case
.
In that case
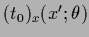 is only needed for
is only needed for 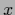 =
= 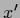 and we may thus directly write
and we may thus directly write
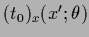 =
=
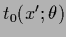 .
As example, consider the following prior energy,
where the
.
As example, consider the following prior energy,
where the 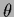 -dependent template
is located in a term with
-dependent template
is located in a term with 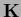 =
= 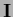 and another, say smoothness, prior is added
with zero template
and another, say smoothness, prior is added
with zero template
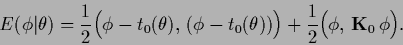 |
(517) |
Combining both terms yields
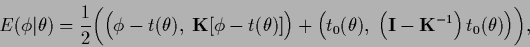 |
(518) |
with effective template and effective inverse covariance
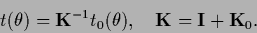 |
(519) |
For differential operators 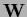 the effective
the effective 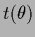 is thus a smoothed version of
is thus a smoothed version of 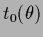 .
.
The extreme case would be to treat
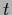 and
and 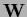 itself as unrestricted hyperparameters.
Notice, however, that increasing flexibility tends to lower
the influence of the corresponding prior term.
That means,
using completely free templates and covariances
without introducing additional restricting hyperpriors,
just eliminates the corresponding prior term
(see Section 5.2.3).
itself as unrestricted hyperparameters.
Notice, however, that increasing flexibility tends to lower
the influence of the corresponding prior term.
That means,
using completely free templates and covariances
without introducing additional restricting hyperpriors,
just eliminates the corresponding prior term
(see Section 5.2.3).
Hence, to restrict the flexibility,
typically a smoothness hyperprior may be imposed
to prevent highly oscillating functions 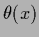 .
For real
.
For real 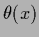 , for example, a smoothness prior
like
, for example, a smoothness prior
like
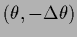 can be used
in regions where it is defined.
(The space of
can be used
in regions where it is defined.
(The space of 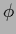 -functions
for which a smoothness prior
-functions
for which a smoothness prior
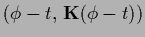 with discontinuous
with discontinuous 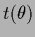 is defined
depends on the locations of the discontinuities.)
An example of a non-Gaussian hyperprior is,
is defined
depends on the locations of the discontinuities.)
An example of a non-Gaussian hyperprior is,
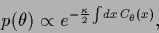 |
(520) |
where 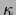 is some constant
and
is some constant
and
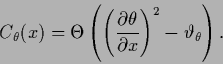 |
(521) |
is zero at locations where the square of the first derivative
is smaller than a certain
threshold
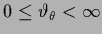 ,
and one otherwise.
(The step function
,
and one otherwise.
(The step function 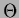 is defined as
is defined as 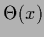 = 0 for
= 0 for 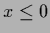 and
and 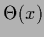 = 1 for
= 1 for 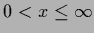 .)
To enable differentiation
the step function
.)
To enable differentiation
the step function 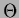 could be replaced by a sigmoidal function.
For discrete
could be replaced by a sigmoidal function.
For discrete 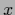 one can analogously count the number of jumps
larger than a given threshold.
Similarly, one may penalize the number
one can analogously count the number of jumps
larger than a given threshold.
Similarly, one may penalize the number 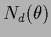 of discontinuities
where
of discontinuities
where
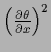 =
= 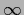 and use
and use
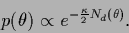 |
(522) |
In the case of a binary field
this corresponds
to counting
the number of times the field changes its value.
The expression 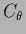 of Eq. (521)
can be generalized to
of Eq. (521)
can be generalized to
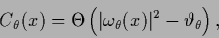 |
(523) |
where,
analogously to Eq. (500),
![\begin{displaymath}
\omega_\theta(x)
=
\int \!dx^\prime \,
{\bf W}_\theta(x,x^\prime)
[\theta(x^\prime)-t_\theta(x^\prime)]
,
\end{displaymath}](img1819.png) |
(524) |
and
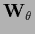 is some filter operator acting on the hyperfield
and
is some filter operator acting on the hyperfield
and
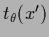 is a template for the hyperfield.
is a template for the hyperfield.
Discontinuous functions 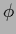 can either be approximated
by using discontinuous templates
can either be approximated
by using discontinuous templates 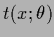 or by eliminating matrix elements of the inverse covariance
which connect the two sides of the discontinuity.
For example, consider the discrete version
of a negative Laplacian
with periodic boundary conditions,
or by eliminating matrix elements of the inverse covariance
which connect the two sides of the discontinuity.
For example, consider the discrete version
of a negative Laplacian
with periodic boundary conditions,
 |
(525) |
and possible square root,
 |
(526) |
The first three points
can be disconnected from the last three points
by setting
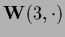 and
and
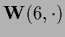 to zero, namely,
to zero, namely,
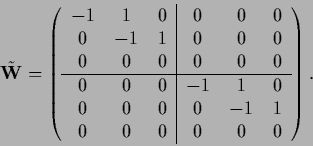 |
(527) |
so that
the smoothness prior with inverse covariance
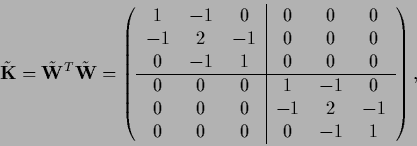 |
(528) |
is ineffective
between points from different regions,
In contrast to using discontinuous templates,
the height of the jump at the discontinuity
has not to be given in advance
when
using such disconnected Laplacians (or other inverse covariances).
On the other hand
training data are then required for all separated regions
to determine the free constants
which correspond to the zero modes of the Laplacian.
Non-Gaussian priors,
which will be discussed in more detail in the next Section,
often provide an alternative
to the use of function hyperparameters.
Similarly to Eq. (521)
one may for example
define a binary function 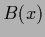 in terms of
in terms of 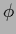 ,
,
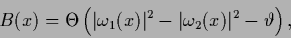 |
(529) |
like, for a negative Laplacian prior,
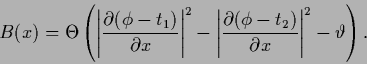 |
(530) |
Here 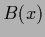 is directly determined by
is directly determined by 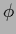 and is not considered as an independent hyperfield.
Notice also that the functions
and is not considered as an independent hyperfield.
Notice also that the functions 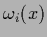 and
and 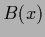 may be nonlocal with respect to
may be nonlocal with respect to 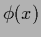 ,
meaning they may depend on more than one
,
meaning they may depend on more than one 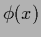 value.
The threshold
value.
The threshold 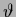 has to be related to
the prior expectations on
has to be related to
the prior expectations on 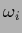 .
A possible non-Gaussian prior for
.
A possible non-Gaussian prior for 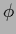 formulated in terms of
formulated in terms of 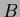 can be,
can be,
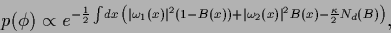 |
(531) |
with
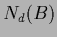 counting the number of discontinuities of
counting the number of discontinuities of 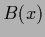 .
Alternatively to
.
Alternatively to 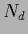 one may for a real
one may for a real 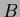 define,
similarly to (523),
define,
similarly to (523),
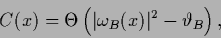 |
(532) |
with
![\begin{displaymath}
\omega_B(x)
=
\int \!dx^\prime \,
{\bf W}_B(x,x^\prime)
[B(x^\prime)-t_B(x^\prime)]
,
\end{displaymath}](img1838.png) |
(533) |
and some filter operator
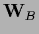 and template
and template
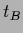 .
Similarly to the introduction of hyperparameters,
one can treat
.
Similarly to the introduction of hyperparameters,
one can treat
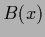 formally as an independent function
by including a term
formally as an independent function
by including a term
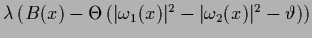 in the prior energy
and taking the limit
in the prior energy
and taking the limit
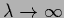 .
.
Eq. (531) looks similar to
the combination of the prior (504)
with the hyperprior (522),
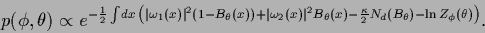 |
(534) |
Notice, however, that the definition (505) of
the hyperfield 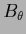 (and
(and 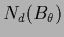 or
or 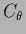 , respectively),
is different from that of
, respectively),
is different from that of 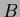 (and
(and 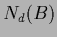 or
or 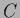 ),
which are direct functions of
),
which are direct functions of 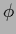 .
If the
.
If the 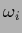 differ only in their templates,
the normalization term can be skipped.
Then, identifying
differ only in their templates,
the normalization term can be skipped.
Then, identifying 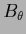 in (534)
with a binary
in (534)
with a binary 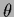 and assuming
and assuming
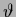 =
= 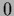 ,
,
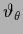 =
= 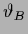 ,
,
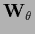 =
= 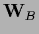 ,
the two equations are equivalent
for
,
the two equations are equivalent
for
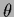 =
=
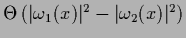 .
In the absence of hyperpriors,
it is indeed easily seen
that this is a selfconsistent solution for
.
In the absence of hyperpriors,
it is indeed easily seen
that this is a selfconsistent solution for 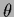 ,
given
,
given 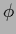 .
In general, however, when
hyperpriors are included,
another solution for
.
In general, however, when
hyperpriors are included,
another solution for 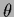 may have a larger posterior.
Non-Gaussian priors will be discussed
in Section 6.5.
may have a larger posterior.
Non-Gaussian priors will be discussed
in Section 6.5.
Hyperpriors or non-Gaussian prior terms
are useful to enforce specific
global constraints for 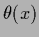 or
or 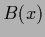 .
In images, for example, discontinuities
are expected to form closed curves.
Hyperpriors, organizing discontinuities along lines or closed curves,
are thus important for image segmentation
[70,153,66,67,238,247].
.
In images, for example, discontinuities
are expected to form closed curves.
Hyperpriors, organizing discontinuities along lines or closed curves,
are thus important for image segmentation
[70,153,66,67,238,247].




Next: Non-Gaussian prior factors
Up: Parameterizing priors: Hyperparameters
Previous: Integer hyperparameters
Contents
Joerg_Lemm
2001-01-21
![]() considered so far have been real or integer numbers,
or vectors with real or integer components
considered so far have been real or integer numbers,
or vectors with real or integer components ![]() .
With the unrestricted template functions of Sect. 5.2.3
or the functions parameterizing the inverse covariance
in Section 5.3.3,
we have, however, also already encountered
function hyperparameters or hyperfields.
In this section we will now discuss
function hyperparameters in more detail.
.
With the unrestricted template functions of Sect. 5.2.3
or the functions parameterizing the inverse covariance
in Section 5.3.3,
we have, however, also already encountered
function hyperparameters or hyperfields.
In this section we will now discuss
function hyperparameters in more detail.
![]() being the (continuous) analogue of vector components
being the (continuous) analogue of vector components ![]() .
In numerical calculations, in particular,
functions usually have to be discretized,
so, numerically, functions stand for high dimensional vectors.
.
In numerical calculations, in particular,
functions usually have to be discretized,
so, numerically, functions stand for high dimensional vectors.
![]() and, for general density estimation, also the dependent variables
and, for general density estimation, also the dependent variables ![]() .
Such functions
.
Such functions ![]() or
or ![]() will be called
local hyperparameters or local hyperfields.
Local hyperfields
will be called
local hyperparameters or local hyperfields.
Local hyperfields ![]() can be used, for example,
to adapt templates or inverse covariances locally.
(For general density estimation problems
replace here and in the following
can be used, for example,
to adapt templates or inverse covariances locally.
(For general density estimation problems
replace here and in the following ![]() by
by ![]() .)
.)
![]() we express real symmetric, positive (semi-)definite inverse covariances
by square roots or ``filter operators''
we express real symmetric, positive (semi-)definite inverse covariances
by square roots or ``filter operators'' ![]() ,
,
![]() =
=
![]() =
=
![]() where
where
![]() represents the vector
represents the vector
![]() .
Thus, in components
.
Thus, in components
![$\displaystyle \int\! dx\,dx^\prime\,
[\phi(x)-t(x)]
\, {\bf K}^T(x,x^{\prime}) \,
[\phi(x^{\prime})-t(x^{\prime})]$](img1747.png)
![$\displaystyle \int\! dx\,dx^\prime\, dx^{\prime\prime}\,
[\phi(x)-t(x)]
{\bf W}^T(x,x^{\prime})$](img1748.png)
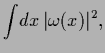
![]() a local adaption of the functions
a local adaption of the functions
![]() as in Eq. (503)
can be achieved by switching
locally between alternative templates
or alternative filter operators
as in Eq. (503)
can be achieved by switching
locally between alternative templates
or alternative filter operators ![]()
![]() to an inverse covariance
to an inverse covariance
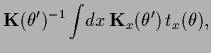
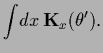
![]() by adapting templates
in prior terms where
by adapting templates
in prior terms where ![]() is equal to the identity
is equal to the identity ![]() .
In that case
.
In that case
![]() is only needed for
is only needed for ![]() =
= ![]() and we may thus directly write
and we may thus directly write
![]() =
=
![]() .
As example, consider the following prior energy,
where the
.
As example, consider the following prior energy,
where the ![]() -dependent template
is located in a term with
-dependent template
is located in a term with ![]() =
= ![]() and another, say smoothness, prior is added
with zero template
and another, say smoothness, prior is added
with zero template
![]() and
and ![]() itself as unrestricted hyperparameters.
Notice, however, that increasing flexibility tends to lower
the influence of the corresponding prior term.
That means,
using completely free templates and covariances
without introducing additional restricting hyperpriors,
just eliminates the corresponding prior term
(see Section 5.2.3).
itself as unrestricted hyperparameters.
Notice, however, that increasing flexibility tends to lower
the influence of the corresponding prior term.
That means,
using completely free templates and covariances
without introducing additional restricting hyperpriors,
just eliminates the corresponding prior term
(see Section 5.2.3).
![]() .
For real
.
For real ![]() , for example, a smoothness prior
like
, for example, a smoothness prior
like
![]() can be used
in regions where it is defined.
(The space of
can be used
in regions where it is defined.
(The space of ![]() -functions
for which a smoothness prior
-functions
for which a smoothness prior
![]() with discontinuous
with discontinuous ![]() is defined
depends on the locations of the discontinuities.)
An example of a non-Gaussian hyperprior is,
is defined
depends on the locations of the discontinuities.)
An example of a non-Gaussian hyperprior is,
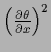 =
= ![]() of Eq. (521)
can be generalized to
of Eq. (521)
can be generalized to
![]() can either be approximated
by using discontinuous templates
can either be approximated
by using discontinuous templates ![]() or by eliminating matrix elements of the inverse covariance
which connect the two sides of the discontinuity.
For example, consider the discrete version
of a negative Laplacian
with periodic boundary conditions,
or by eliminating matrix elements of the inverse covariance
which connect the two sides of the discontinuity.
For example, consider the discrete version
of a negative Laplacian
with periodic boundary conditions,




![]() in terms of
in terms of ![]() ,
,
![]() or
or ![]() .
In images, for example, discontinuities
are expected to form closed curves.
Hyperpriors, organizing discontinuities along lines or closed curves,
are thus important for image segmentation
[70,153,66,67,238,247].
.
In images, for example, discontinuities
are expected to form closed curves.
Hyperpriors, organizing discontinuities along lines or closed curves,
are thus important for image segmentation
[70,153,66,67,238,247].