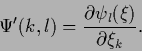Next: Linear trial spaces
Up: Parameterizing likelihoods: Variational methods
Previous: General parameterizations
Contents
Gaussian priors for parameters
Up to now we assumed the prior to be given for a function
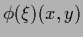 depending on
depending on  and
and  .
Instead of a prior in a function
.
Instead of a prior in a function
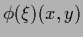 also a prior in another not
also a prior in another not 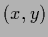 -dependent function
of the parameters
-dependent function
of the parameters 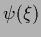 can be given.
A Gaussian prior in
can be given.
A Gaussian prior in
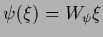 being a linear function of
being a linear function of 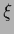 ,
results in a prior which is also Gaussian in
the parameters
,
results in a prior which is also Gaussian in
the parameters 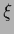 , giving a regularization term
, giving a regularization term
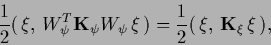 |
(371) |
where 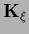 =
=
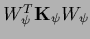 is not an operator in a space of functions
is not an operator in a space of functions 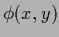 but a matrix in the space of parameters
but a matrix in the space of parameters 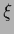 .
The results of Section 4.1
apply to this case provided the following replacement is made
.
The results of Section 4.1
apply to this case provided the following replacement is made
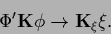 |
(372) |
Similarly,
a nonlinear 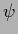 requires the replacement
requires the replacement
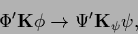 |
(373) |
where
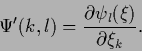 |
(374) |
Thus, in the general case where a Gaussian (specific) prior in
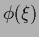 and
and 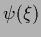 is given,
is given,
or, including also non-zero template functions (means)
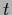 ,
, 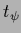 for
for 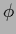 and
and 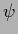 as discussed in Section 3.5,
as discussed in Section 3.5,
The 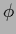 and
and 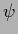 -terms of the energy
can be interpreted as corresponding to
a probability
-terms of the energy
can be interpreted as corresponding to
a probability
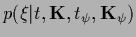 ,
(
,
(
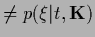
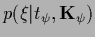 ),
or, for example,
to
),
or, for example,
to
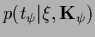
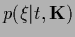 with one of the two terms term
corresponding to a Gaussian likelihood
with
with one of the two terms term
corresponding to a Gaussian likelihood
with 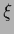 -independent normalization.
-independent normalization.
The stationarity equation becomes
which defines 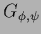 ,
and for
,
and for 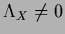
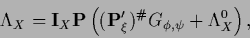 |
(379) |
for
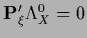 .
.
Table 5:
Summary of stationarity equations.
For notations, conditions and comments see
Sections
3.1.1,
3.2.1,
3.3.2,
3.3.1,
4.1
and 4.2.
| Variable |
Error |
Stationarity equation |
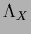 |
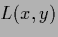 |
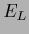 |
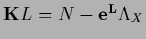 |
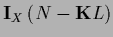 |
 |
 |
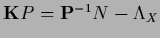 |
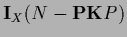 |
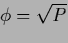 |
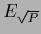 |
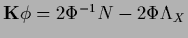 |
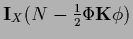 |
 |
 |
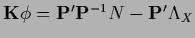 |
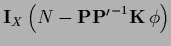 |
 |
 |
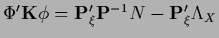 |
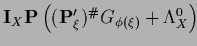 |
 |
 |
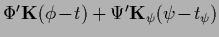 |
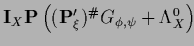 |
| |
|
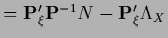 |
|
|




Next: Linear trial spaces
Up: Parameterizing likelihoods: Variational methods
Previous: General parameterizations
Contents
Joerg_Lemm
2001-01-21
![]() depending on
depending on ![]() and
and ![]() .
Instead of a prior in a function
.
Instead of a prior in a function
![]() also a prior in another not
also a prior in another not ![]() -dependent function
of the parameters
-dependent function
of the parameters ![]() can be given.
A Gaussian prior in
can be given.
A Gaussian prior in
![]() being a linear function of
being a linear function of ![]() ,
results in a prior which is also Gaussian in
the parameters
,
results in a prior which is also Gaussian in
the parameters ![]() , giving a regularization term
, giving a regularization term